In questo articolo spiegheremo cosa sono le disequazioni concentrandoci in particolar modo sulle disequazioni di primo grado. Infine vedremo insieme due esempi di risoluzione di esercizi sulle disequazioni di primo grado passo-passo.
Impareremo inoltre a conoscere la differenza fondamentale che vi è tra una disequazione ed una equazione di primo grado oltre ad alcuni principi fondamentali da tenere a mente per la risoluzione delle disequazioni.
Che cosa sono le disequazioni di primo grado
In matematica una disequazione è in generale una diseguaglianza tra due membri.
ESEMPI DI DISEQUAZIONI DI PRIMO GRADO POSSONO ESSERE
Notiamo che sussiste, a differenza delle equazioni, il segno di diseguaglianza tra i membri, pertanto una disequazione, in generale, a differenza di una equazione, non è soddisfatta da un unico valore di x, ma da un insieme di valori di x.
Risolvere una disequazione vuol dire molto semplicemente riuscire a trovare l’intervallo dei valori di x che rendono VERA la diseguaglianza.
Inoltre una disequazione si dice di primo grado se la variabile (solitamente indicata con la lettera x) figura nella diseguaglianza, al più, al primo esponente.
SIAMO ANCHE SU YOU TUBE
Video tutorial con spiegazione
Nel video qui sotto troverai una spiegazione dettagliata, pensata per chi vuole imparare in modo semplice e veloce. Il metodo mostrato è adatto a studenti delle scuole medie e superiori, ma anche a chi desidera un ripasso rapido ed efficace.
👉 Guarda il video e segui gli esercizi proposti: ti aiuteranno a fissare i passaggi fondamentali per non sbagliare.
Argomenti trattati nel video
- Definizione di disequazioni di primo grado
- Procedura passo passo per la risoluzione
- Errori più comuni da evitare
- Esempi commentati
- Esercizi svolti con soluzioni
CAPITOLI
00:00 Introduzione
00:18 Che cos’è una disequazione di primo grado
01:13 Proprietà delle disequazioni di primo grado
02:53 Come risolvere una disequazione di primo grado
03:59 Verifica della disequazione
05:22 Grafico delle soluzioni
07:59 Esercizi svolti disequazioni di primo grado
10:42 Esercizi da risolvere
🔔 Resta aggiornato! VISITA IL NOSTRO CANALE YOU TUBE e non dimenticare di ISCRIVERTI 🙂
VEDI ANCHE
Principi da ricordare per la risoluzione di una disequazione
- Aggiungendo o sottraendo da ambo i membri di una disequazione una stessa quantità, si ottiene una disequazione dello stesso senso.
- Moltiplicando o dividendo ambo i membri di una disequazione per uno stesso numero positivo, si ottiene una disequazione dello stesso senso.
- Moltiplicando o dividendo ambo i membri di una disequazione per uno stesso numero negativo, si ottiene una disequazione di senso contrario.
Esempi di disequazioni di primo grado risolte
ESEMPIO 1
Risolvere la seguente disequazione:
per prima cosa calcoliamo il minimo comune multiplo per ciascuno dei due membri separatamente: tra 3 e 4 si ha che m.c.m.(3, 4)=12, mentre a primo membro il m.c.m. è pari a 5, si ha pertanto:
eliminiamo i denominatori (il verso della disequazione non cambia perché stiamo moltiplicando per 5 e per 12 che sono entrambi di segno positivo)
semplifichiamo
portiamo adesso tutti i termini simili a primo membro ed i termini noti a secondo membro:
e quindi sommando i termini
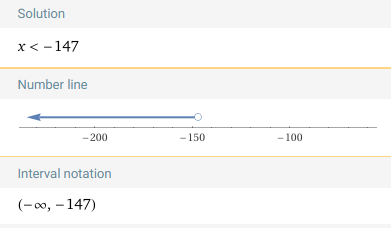
che rappresenta la soluzione della disequazione. Troviamo quindi che la disequazione data viene soddisfatta non per un solo valore o per alcuni valori di x, ma per tutti i valori di x minori di -147.
RAPPRESENTAZIONE GRAFICA DELLA SOLUZIONE
ESEMPIO 2
Risolvere la seguente disequazione:
calcoliamo il mcm a 2° membro
moltiplichiamo ambo i membri per 18
isoliamo i termini con la x a primo membro e i termini noti a secondo membro
moltiplichiamo ambo i membri per -1 ricordando di invertire il senso della diseguaglianza
che rappresenta la soluzione della disequazione. Avremo quindi che la disequazione data viene soddisfatta non per un solo valore o per alcuni valori di x, ma per tutti i valori di x maggiori o uguali di 39/35, appartenenti quindi all’insieme
oppure, il che è lo stesso,
all’intervallo
RAPPRESENTAZIONE GRAFICA DELLA SOLUZIONE


