Le disequazioni frazionarie sono disequazioni contenenti alcuni termini in cui l’incognita compare al denominatore.
Una disequazione frazionaria assume per esempio una forma del tipo
ove con N(x) si è indicato il numeratore, mentre D(x) rappresenta il denominatore dell’equazione. Risolvere tale disequazione fratta vuol dire quindi ricercare l’insieme dei valori della x (che rappresenta la variabile indipendente o l’incognita) che rendono vera la diseguaglianza, in questo caso il primo membro maggiore o uguale a zero.
Potrebbe anche aversi per esempio un ulteriore caso rappresentato dalla seguente disequazione algebrica fratta:
In tale caso il primo membro deve risultare minore di zero.
Risolvere una disequazione frazionaria (o fratta) vuol dire molto semplicemente riuscire a trovare l’insieme dei valori della x che verificano (o rendono vera) la disequazione.
Per poter risolvere una disequazione frazionaria si procede nel modo che indicheremo nel paragrafo successivo.
PROCEDURA DA SEGUIRE PER RISOLVERE LE DISEQUAZIONI FRATTE
- Si riporta la disequazione assegnata in una delle seguenti forme:
- N(x)/D(x) ≥ 0
- N(x)/D(x) ≤ 0
- N(x)/D(x) > 0
- N(x)/D(x) < 0
- Si studia separatamente il segno del numeratore N(x) e del denominatore D(x) della disequazione frazionaria.
- Si rappresenta graficamente l’insieme delle soluzioni del numeratore e del denominatore separatamente e poi si procede ad eseguire il rapporto delle soluzioni.
Per comprendere meglio vediamo di seguito di risolvere insieme passo-passo una serie di esercizi contenenti disequazioni frazionarie cercando di comprendere il modus operandi nel momento in cui ci si trova a risolvere questa particolare tipologia di disequazioni.
POTREBBE ANCHE INTERESSARTI
ESERCIZI SVOLTI SULLE DISEQUAZIONI FRAZIONARIE
ESERCIZIO SVOLTO N.1
Risolvere la disequazione
SOLUZIONE
Per prima cosa poniamo la disequazione nella forma N(x)/D(x)≥0; si avrà quindi
calcoliamo il m.c.m.
si ha così:
N(x)=7x-4 e D(x)=5x-1
Ricerchiamo adesso per quali valori di x il numeratore ed il denominatore sono, ad esempio, positivi e poi, affinché la disequazione sia verificata, per quali valori N(x) e D(x) risultano concordi.
Poniamo quindi
da cui
dopodiché poniamo
D(x)>0
5x-1>0
che ha per soluzione
N.B. Il denominatore deve porsi maggiore di zero e non maggiore o uguale in quanto l’annullamento del denominatore farebbe perdere di significato la disequazione.
A questo punto possiamo riportare le due soluzioni separatamente su un diagramma e fare il rapporto N(x)/D(x).
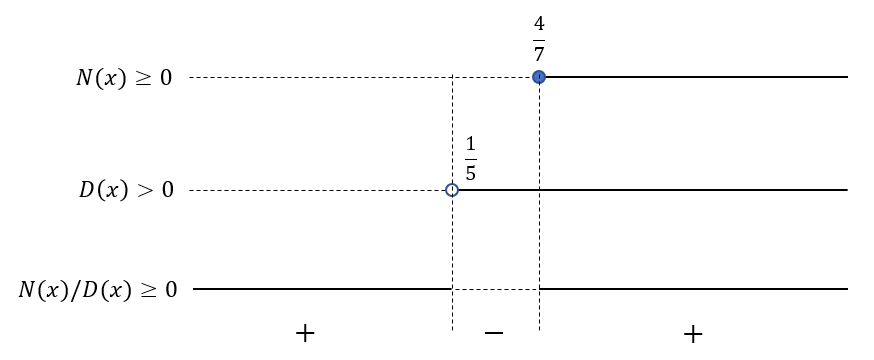
Notiamo che per x compreso tra -inf ed 1/5 (escluso) sia N che D sono entrambi negativi e quindi, risultando positivo il rapporto di due numeri negativi, la disequazione risulta verificata.
Nell’intervallo compreso tra 1/5 e 4/7 (incluso) il numeratore N(x) risulta negativo mentre il denominatore è positivo, pertanto il rapporto risulterà negativo (disequazione non verificata).
Infine, nell’intervallo 4/7 (incluso) +inf sia N che D sono entrambi positivi e pertanto il loro rapporto è positivo; in tale intervallo la disequazione risulta quindi verificata.
Dal grafico sopra e dalle osservazioni fatte possiamo certamente concludere che l’insieme delle soluzioni della disequazione è dato dall’intervallo:
Rappresentazione grafica della soluzione:
ESERCIZIO SVOLTO N.2
Risolvere la disequazione
SOLUZIONE
Per prima cosa notiamo che il numeratore è un numero negativo. Affinché il rapporto N/D risulti minore di zero deve necessariamente aversi D>0, quindi scriveremo
da cui
L’insieme delle soluzioni delle disequazione è pertanto l’intervallo aperto:
Rappresentazione grafica della soluzione:
ESERCIZIO SVOLTO N.3
Risolvere la disequazione
SOLUZIONE
Portando il 3 a primo membro ed eseguendo il m.c.m. la disequazione può essere scritta nella seguente forma:
Studiamo adesso separatamente il numeratore N(x) ed il denominatore D(x) imponendo per ciascuno di essi che siano, per esempio, positivi:
N(x)>0 -> 2-3x>0 -> x<2/3
D(x)>0 -> x>0
Riportiamo come di consueto le due soluzioni separatamente su un diagramma per poi fare il rapporto N(x)/D(x).
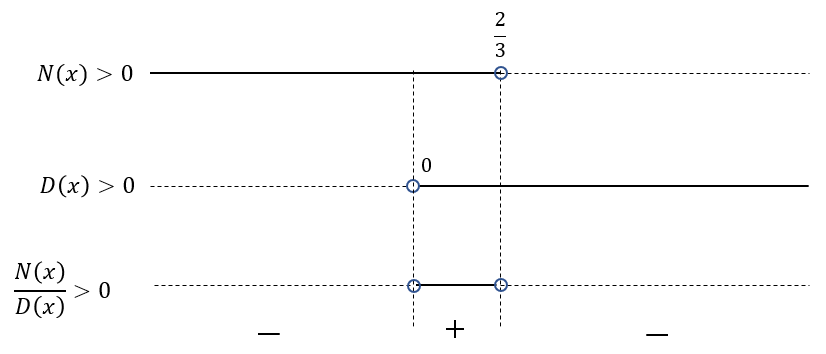
Possiamo notare che l’insieme in cui la disequazione è negativa è rappresentato dall’insieme
Rappresentazione grafica della soluzione:
ESERCIZIO SVOLTO N.4
Risolvere la disequazione
SOLUZIONE
Calcoliamo il m.c.m. dopo aver riportato tutto a primo membro:
raccogliendo al numeratore si ha:
Studiamo come al solito separatamente il numeratore N(x) ed il denominatore D(x) imponendo per ciascuno di essi che siano, per esempio, positivi:
N(x)>0
da cui
mentre per quanto riguarda il denominatore deve aversi
D(x)>0 -> x>0
Riportiamo nuovamente le soluzioni in maniera separata su un diagramma per poi procedere al rapporto N(x)/D(x).
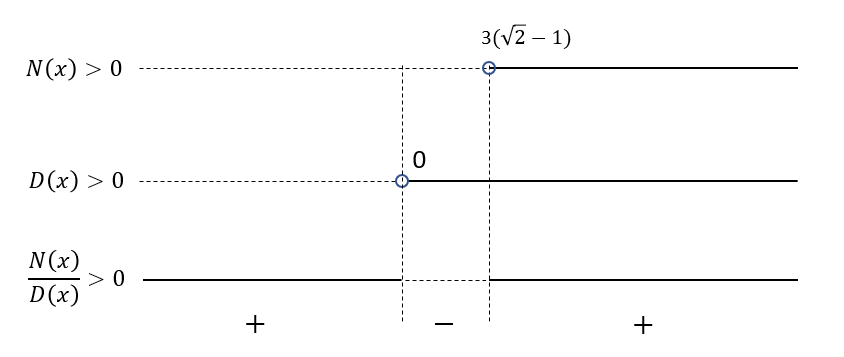
Notiamo che l’insieme in cui la disequazione è negativa è rappresentato dall’intervallo:
Rappresentazione grafica della soluzione:
ESERCIZIO SVOLTO N.5
Risolvere la disequazione
In questo caso notiamo che sia il numeratore che il denominatore sono entrambi delle espressioni polinomiali, in particolare troviamo il prodotto di polinomi.
In questo caso la procedura è analoga agli esercizi già visti con la differenza che N(x) e D(x) verranno studiati come il prodotto di due polinomi.
Studiamo separatamente N(x) e D(x);
Per N(x)>0 si ha:
(1-x)(2x-1)>0
che risulta positivo se e soltanto se entrambi i termini entro parentesi sono concordi.
Possiamo quindi risolvere separatamente le disequazioni imponendo
1-x>0 e 2x-1>0
le cui soluzioni sono rispettivamente:
x<1 e x>1/2
Vediamo di chiarire meglio il tutto con il seguente diagramma:
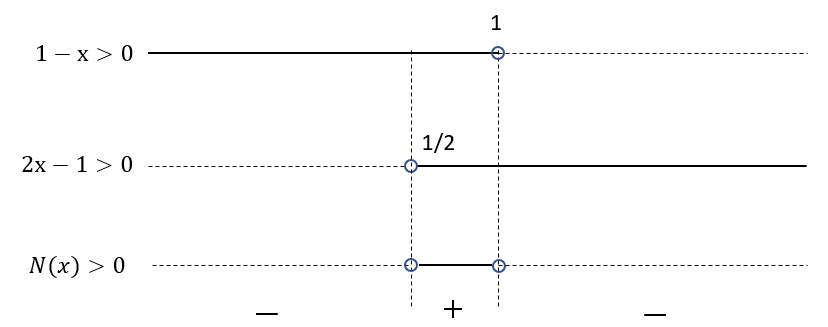
A questo punto effettuiamo lo studio del denominatore D(x) della disequazione frazionaria.
Per D(x)>0 si ha:
x(3x-1)>0
Ponendo
x>0 e 3x-1>0
si ottengono le soluzioni
x>0 e x>1/3
Tracciamo il diagramma relativo allo studio del denominatore:
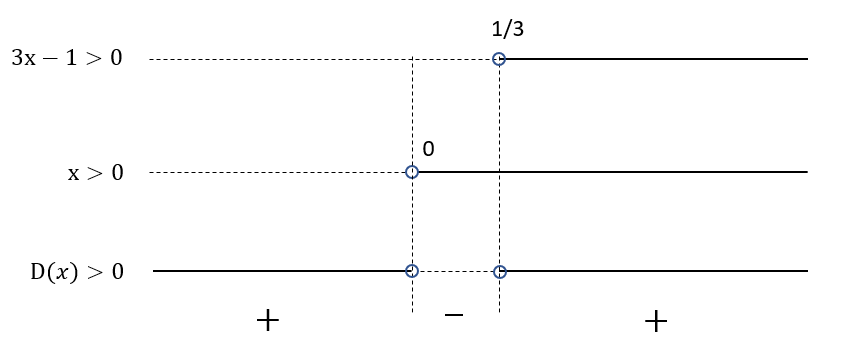
Siamo pronti a questo punto per effettuare lo studio del segno della disequazione frazionaria, ovvero del rapporto N(x)/D(x) servendoci di un grafico che riportiamo qui di seguito:
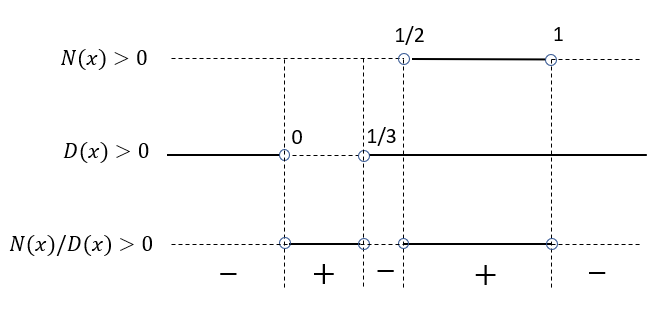
La disequazione fratta di partenza risulta così positiva nell’intervallo
che rappresenta la soluzione al problema dato.
Se hai un dubbio sugli esercizi svolti o un problema sulle disequazioni frazionarie faccelo sapere nei commenti qui in basso o via email, saremo lieti di darti una mano.
Alla prossima!
