Oggi vedremo insieme in maniera semplice e pratica come risolvere un’equazione di secondo grado.
Consideriamo l’equazione di secondo grado scritta nella forma:
con
Sappiamo dalla teoria elementare dell’algebra che tale equazione ammette le seguenti soluzioni:
e quindi in altre parole avremo:
e
con
che rappresenta il delta dell’equazione.
OSSERVAZIONI
- Si comprende molto chiaramente che le soluzioni sono 2 (data la presenza del segno “+” o “-” prima della radice)
- è sufficiente conoscere i valori a,b, e c per trovare le soluzioni x1 ed x2 (o zeri) dell’equazione di secondo grado
Notiamo che, affinché l’equazione di secondo grado ammetta soluzione nel campo dei numeri reali, è necessario che il radicale sia maggiore o uguale a zero: deve risultare pertanto anche il radicando maggiore o uguale a zero. Viceversa l’equazione non ammette soluzione nel campo dei numeri reali ma ammetterà soluzione nel campo dei numeri immaginari.
Vediamo quindi nel dettaglio le varie condizioni:
CASO I – DELTA MAGGIORE DI ZERO
In questo caso l’equazione ammette due soluzioni reali e distinte nel campo dei numeri reali
CASO II – DELTA UGUALE A ZERO
Quando il discriminante (o delta) è uguale a zero l’equazione di secondo grado ammette sempre due soluzioni nel campo dei numeri reali, ma tali soluzioni risultano coincidenti
CASO III – DELTA MINORE DI ZERO
In tal caso l’equazione ammette una soluzione appartenente al campo dei numeri immaginari (in particolare le radici dell’equazione risultano complesse e coniugate).
ESEMPI di come risolvere un’equazione di secondo grado
Vediamo adesso di chiarire meglio il tutto con un esempio pratico analizzando i vari casi:
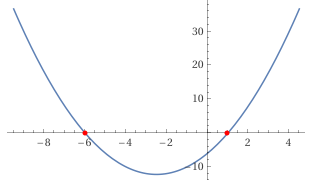
ESEMPIO CASO I – DELTA MAGGIORE DI ZERO
Consideriamo l’equazione
Dal confronto con l’equazione vista all’inizio dell’articolo avremo certamente: a=1, b=5, c=-6.
Procedendo con il calcolo del delta si ottiene:
Le soluzioni in tal caso sono:
e quindi
e
Nella figura che segue possiamo notare le due soluzioni reali e distinte.
ESEMPIO CASO II – DELTA UGUALE A ZERO
Consideriamo l’equazione
Per tale equazione avremo che: a=1, b=4, c=4.
Calcoliamo quindi il delta:
Con delta uguale a zero la soluzione si è ridotta a
e quindi sostituendo i valori numerici:
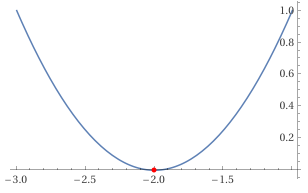
In questo caso la soluzione non è unica, ma le soluzioni x1 ed x2 sono coincidenti e pari a -2 entrambe!
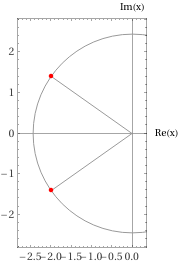
ESEMPIO CASO III – DELTA MINORE DI ZERO
Immaginiamo adesso di voler risolvere la seguente equazione di secondo grado:
Dal confronto con l’equazione vista all’inizio dell’articolo avremo certamente: a=1, b=4, c=6.
Se proviamo a calcolare il delta troveremo:
che è per l’appunto un numero immaginario.
Ecco che in tal caso le soluzioni dell’equazione possono scriversi come:
che rappresentano le due radici complesse coniugate soluzione dell’equazione nel campo dei numeri immaginari.
Nella figura seguente i pallini (in rosso) rappresentano le radici complesse (soluzioni) nel piano di Gauss.
