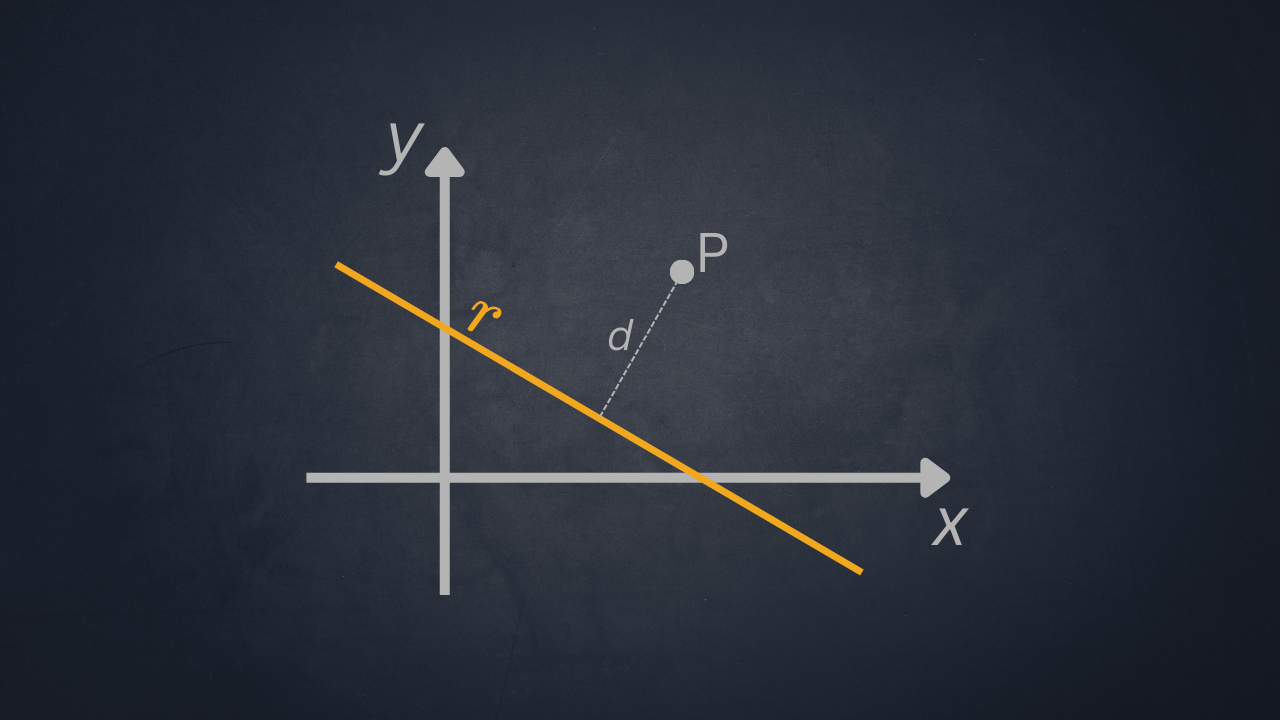
Tra i problemi fondamentali della geometria analitica nel piano cartesiano vi è il calcolo della distanza di un punto da una retta.
Tale esercizio, a prima vista, potrebbe sembrare puramente tecnico, uno di quei calcoli che si risolvono applicando in modo meccanico una formula. In realtà, dietro questo risultato si nasconde un contenuto matematico ben più significativo. La formula della distanza punto–retta costituisce infatti una sintesi elegante di concetti fondamentali come le equazioni lineari, l’interpretazione vettoriale delle rette nel piano e il prodotto scalare.
Quello che appare così come un semplice procedimento di calcolo rappresenta in realtà un punto di incontro tra algebra e geometria.
In questo articolo in particolare, dato un punto \(P(x_0,y_0)\) e una retta \(r\) di equazione \(ax+by+c=0\), vedremo come determinare la distanza minima tra il punto e la retta, cioè la lunghezza del segmento perpendicolare condotto da un punto \(P\) ad una retta \(r\) giacente nel piano.
Più nel dettaglio ci occuperemo anche di fornire:
- La definizione geometrica del problema
- La formula generale per il calcolo della distanza
- Esempi svolti passo per passo
- I casi particolari di rette verticali e orizzontali
- La dimostrazione della formula mediante il prodotto scalare
L’obiettivo quindi non è soltanto saper applicare correttamente una formula, ma comprenderne la struttura e il significato geometrico.
Definizione geometrica della distanza di un punto da una retta
Sia assegnata una retta \(r\) nel piano cartesiano e un punto \(P\) esterno ad essa.
La distanza di \(P\) dalla retta \(r\) può essere pensata come la lunghezza del segmento perpendicolare condotto dal punto alla retta.
In particolare, se indichiamo con \(H\) il piede della perpendicolare tracciata da \(P\) alla retta \(r\), allora la distanza cercata \(d\) è la misura del segmento \(PH\), come in Fig.1.
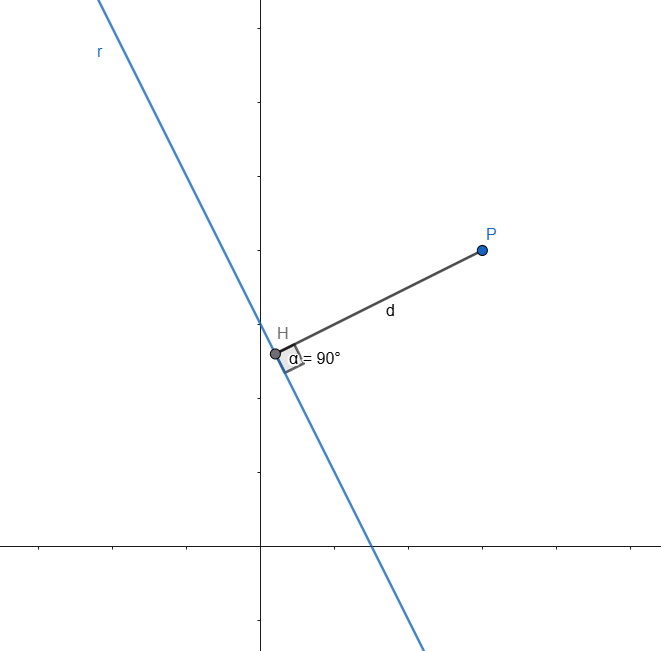
È importante sottolineare che si tratta della distanza minima tra il punto e la retta.
Formula per il calcolo della distanza di un punto da una retta
Siano dati la retta \(r\) in forma implicita
ed il punto
Si può dimostrare (vedasi sezione relativa alla dimostrazione) che la distanza del punto \(P\) dalla retta \(r\) può essere calcolata come:
Notiamo inoltre che se il punto \(P\) coincide con l’origine degli assi \(O\), si avrà:
pertanto la (1) si ridurrà alla seguente forma semplificata:
Interpretazione dei termini
- \(a\) e \(b\) determinano la direzione della retta;
- il numeratore \(ax_0+by_0+c\) misura quanto il punto “si discosta” dall’equazione della retta;
- il denominatore \(\sqrt{a^2 + b^2}\) normalizza tale scostamento;
- il valore assoluto garantisce che la distanza sia non negativa.
Per comprendere pienamente il significato dei coefficienti \(a\), \(b\) e \(c\) nell’equazione \(ax+by+c=0\), è utile richiamare i concetti fondamentali trattati nell’approfondimento dedicato alla retta in geometria analitica.
Ma vediamo adesso come applicare concretamente le formule viste.
Esempi svolti sul calcolo della distanza tra punto e retta
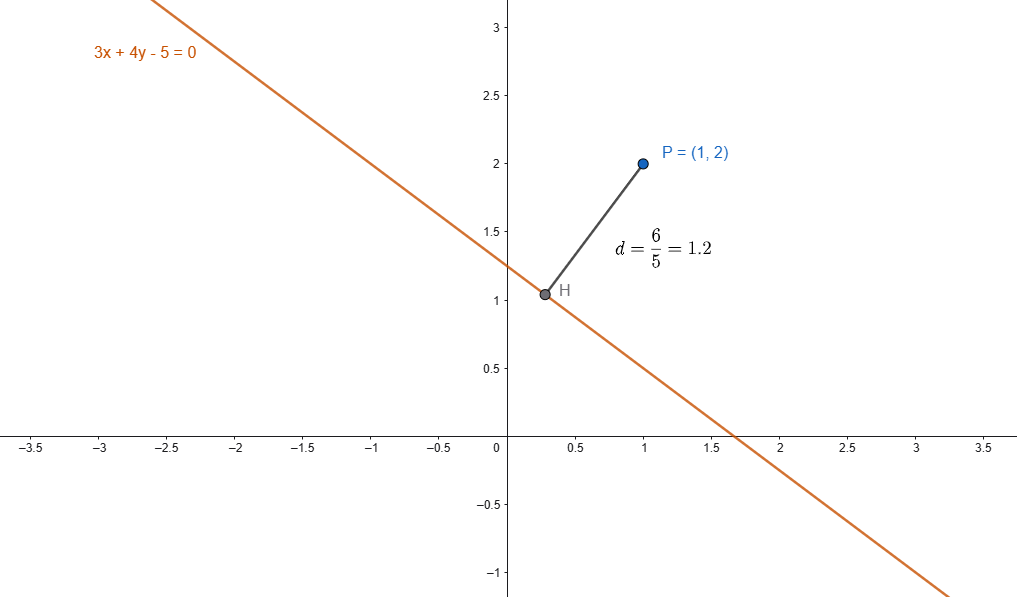
Esempio 1 – Applicazione diretta
Dato il punto \(P(1,2)\) e la retta \(r:\,3x+4y−5=0\), determinare la distanza del punto dalla retta.
SOLUZIONE
Dal momento che la retta è già scritta in forma implicita, è possibile calcolare immediatamente i coefficienti \(a\), \(b\) e \(c\):
Le coordinate del punto \(P\) valgono:
La distanza tra il punto \(P\) e la retta \(r\) può calcolarsi immediatamente applicando la (1) come segue:
Esempio 2 – Punto P appartenente alla retta
Determinare la distanza del punto \(P(2,−1)\) dalla retta \(2x−y−5=0\).
SOLUZIONE
Analogamente a quanto già visto nell’Esempio 1, è possibile calcolare i coefficienti della retta come segue:
Le coordinate del punto \(P\) valgono invece:
La distanza tra il punto \(P\) e la retta può essere calcolata sempre applicando la (1):
In questo caso si è ottenuta una distanza pari a zero, pertanto possiamo concludere che il punto \(P\) appartiene alla retta data.
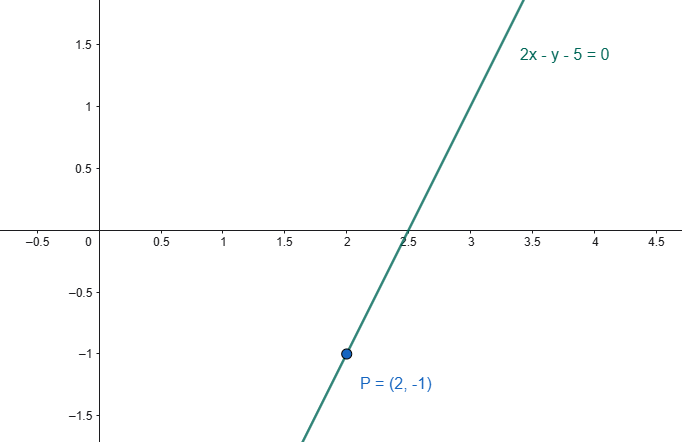
In questo caso la distanza del punto dalla retta è pari a zero risultando P appartenente ad essa.
Esempio 3 – Retta in forma esplicita con punto P coincidente con l’origine degli assi
Dato il punto \(P(0,0)\) e la retta \(y=2x+1\), determinare la distanza del punto \(P\) dalla retta.
In questo caso notiamo che la retta assegnata compare nella formulazione esplicita, pertanto la prima operazione da svolgere è trasformarla in forma implicita;
si ottiene la seguente formulazione implicita:
I coefficienti dell’ultima equazione sono:
Adesso notiamo che il punto \(P\) coincide con l’origine degli assi, pertanto la distanza tra tale punto e la retta potrà essere calcolata applicando la (2) come segue:
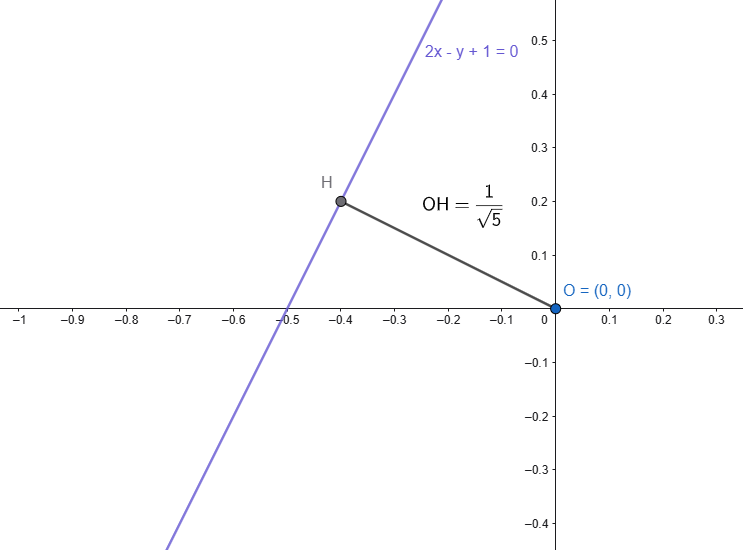
di equazione 2x-y+1=0.
Casi particolari
Retta orizzontale
Se la retta ha equazione
la distanza è:
essendo \(y_0\) l’ordinata del punto \(P(x_0,y_0)\).
Esempio:
Dato il punto \(P(3,2)\) e la retta \(y=5\), la distanza tra il punto e la retta si calcola immediatamente applicando la (3):
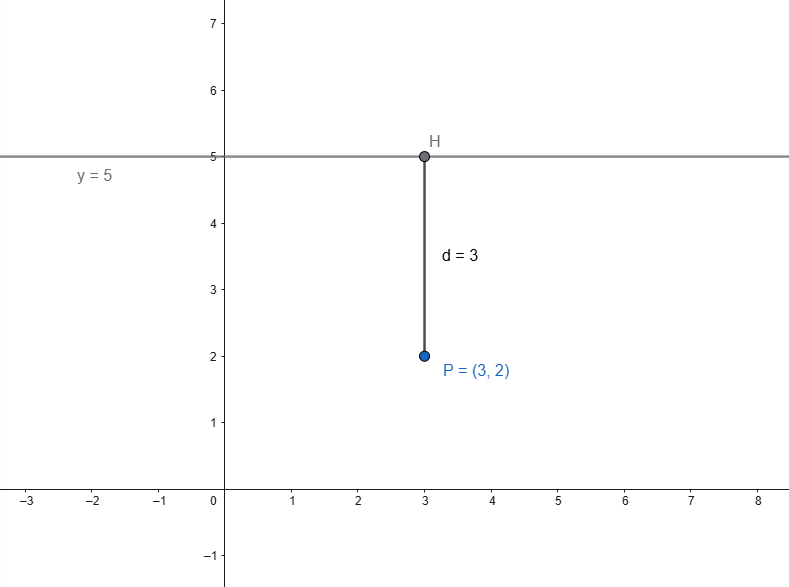
Retta verticale
Se la retta ha equazione
la distanza è:
essendo \(x_0\) l’ascissa del punto \(P(x_0,y_0)\).
Esempio:
Dato il punto \(P(-2,4)\) e la retta di equazione \(x=6\), la distanza tra punto e retta si può calcolare applicando la (4):
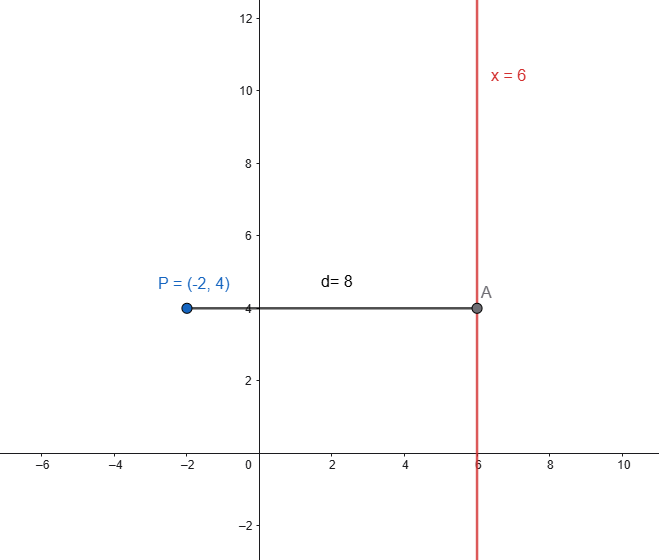
Dimostrazione della formula per il calcolo della distanza di un punto da una retta (approfondimento)
Vediamo ora come si ricava la formula (1) utilizzando i vettori e il prodotto scalare.
1️⃣ Data la retta:
si può dimostrare che
è un vettore normale alla retta data, cioè perpendicolare ad essa.
2️⃣ Sia adesso \(Q(x_1, y_1)\) un punto generico appartenente alla retta data; deve risultare quindi:
3️⃣ Definiamo inoltre il vettore
che collega un generico punto \(P(x_0,y_0)\) del piano al punto \(Q\) sulla retta.
4️⃣ La distanza cercata è la lunghezza della proiezione di \(\vec{PQ}\) sul vettore normale \(\vec{n}\), quindi deve aversi:
5️⃣ Calcolo del prodotto scalare
Sviluppando il prodotto scalare si ha:
che può essere scritta come:
Dalla (7) si ricava immediatamente:
che sostituito alla (11) fornisce:
⚠ Osservazione: il risultato non dipende dal punto \(Q\) scelto sulla retta.
Infatti, se \(Q_1\) e \(Q_2\) sono due punti della retta, allora il vettore \(\vec{Q_1Q_2}\) è parallelo alla retta \(r\) e quindi ortogonale al vettore normale \(\vec{n}\). Di conseguenza, il prodotto scalare (12) non cambia.
6️⃣ Sappiamo inoltre che il modulo del vettore normale vale:
Formula conclusiva
Sostituendo la (12) e la (13) nella (9) si ottiene:
o, il che è lo stesso:
che coincide con la formula (1) precedentemente enunciata e che rappresenta la distanza tra un generico punto del piano \(P\) ed una retta \(r\).
Errori comuni da evitare
- Dimenticare il valore assoluto
- Non ridurre la retta in forma implicita
- Omettere la radice nel denominatore
- Confondere \(a^2 + b^2\) con \(\sqrt{a^2 + b^2}\)
Collegamenti con altri argomenti
Il calcolo della distanza di un punto da una retta è strettamente collegato a:
- prodotto scalare;
- vettori normali;
- proiezione ortogonale;
- distanza tra rette parallele;
- studio delle coniche.
Si tratta di un risultato centrale della geometria analitica, perché mostra come un problema geometrico possa essere risolto attraverso strumenti algebrici in modo efficace.
Conclusione
Il calcolo della distanza di un punto da una retta rappresenta un passaggio fondamentale nello studio della geometria analitica.
La formula è semplice da applicare, ma racchiude una struttura concettuale profonda: nasce dalla nozione di ortogonalità e dall’uso del prodotto scalare.
Imparare ad utilizzarla correttamente negli esercizi e comprenderne la dimostrazione significa consolidare in modo appropriato il rapporto tra algebra e geometria, che costituisce il nucleo della geometria analitica nel piano.