Per risolvere le disequazioni di grado superiore al secondo è possibile seguire la seguente procedura:
- si cerca dapprima di decomporre il polinomio che figura al primo membro quando il secondo è zero in fattori di primo e secondo grado;
- si esaminano i segni di ciascun fattore riportandoli su un grafico;
- si effettua il prodotto dei segni.
Esempi svolti di disequazioni di grado superiore al secondo
Di seguito riportiamo alcuni esercizi svolti passo passo con grafici sulle disequazioni di grado superiore al secondo
Esempio 1
Risolvere la disequazione
Notiamo che l’equazione può scriversi come
A questo punto conviene ricercare i valori di x per i quali ciascun fattore è, per esempio, positivo e poi riporteremo i risultati ottenuti in un diagramma
| Fattore 1 | \[x\] |
| Fattore 2 | \[x^2+9\] |
| Fattore 3 | \[x^2-9\] |
Effettuiamo dapprima, separatamente, lo studio del segno di ciascun fattore.
Dallo studio del segno del Fattore 1 sappiamo che questo è positivo per
Per il Fattore 2 potrà porsi
il quale risulta sempre maggiore di zero.
Effettuando lo studio del Fattore 3 risulta
che è verificata per valori di x<-3 o per valori di x>3.
A questo punto siamo pronti per tracciare il diagramma delle soluzioni dei singoli fattori
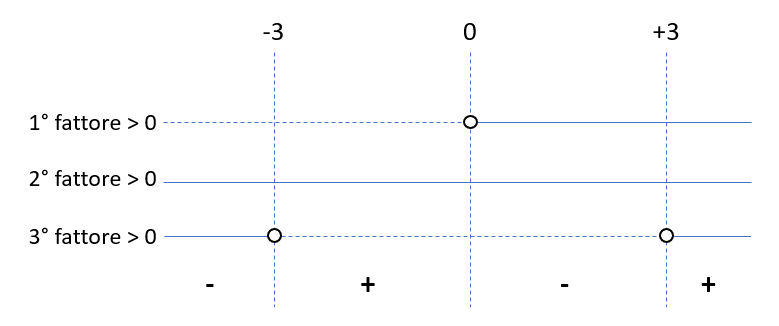
Dal prodotto dei segni si ricava che la disequazione di partenza risulta verificata per:
Esempio 2
Risolvere la disequazione
L’ineguaglianza, dopo aver messo in evidenza x, può scriversi come:
Come per l’esempio visto in precedenza ricerchiamo i valori di x per i quali ciascun fattore è, per esempio, positivo e nuovamente riportiamo i risultati ottenuti in un diagramma.
| Fattore 1 | \[x\] |
| Fattore 2 | \[x^2+3x+2\] |
Dallo studio del segno del Fattore 1 sappiamo che questo è positivo per
Per il Fattore 2 dovrà risolversi dapprima la relativa disequazione associata
Ricerchiamo così gli zeri dell’equazione associata al Fattore 2
da cui
Dalla teoria delle disequazioni di secondo grado sappiamo che la disequazione (associata al Fattore 2) ha le seguenti soluzioni:
Infine tracciamo il grafico delle soluzioni dei singoli fattori e provvediamo ad effettuare il prodotto dei segni
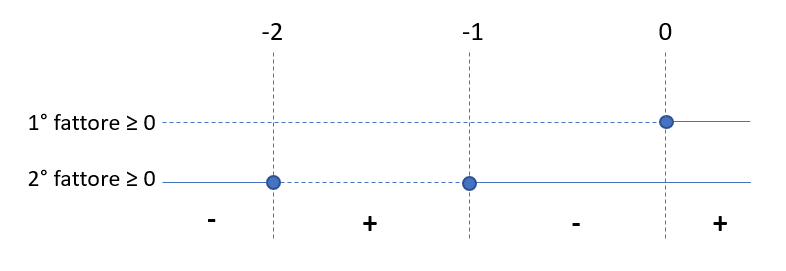
Dal prodotto dei segni si ricava che la disequazione di partenza risulta verificata per:
Esempio 3
Risolvere la disequazione
L’equazione biquadratica associata alla disequazione è
Occorre pertanto risolvere inizialmente tale equazione.
Ponendo
la biquadratica si può scrivere come
che risolta fornisce le seguenti soluzioni
da cui si ottiene, per t1
mentre per t2 si ha che
quest’ultima non ammette soluzione nel campo dei numeri reali.
Alla luce di quanto esposto osserviamo che la disequazione di partenza può essere scritta nella forma
Ricercando i valori di x per i quali ciascun fattore è, per esempio, positivo si ottengono le soluzioni che riportiamo nella tabella seguente
| Fattore 1 > 0 | \[(x^2+1)>0\] | \[\forall x\in\mathbb{R}\] |
| Fattore 2 > 0 | \[(x-\sqrt{3})>0\] | per \[x>\sqrt{3}\] |
| Fattore 3 > 0 | \[(x+\sqrt{3})>0\] | per \[x>-\sqrt{3}\] |
graficamente
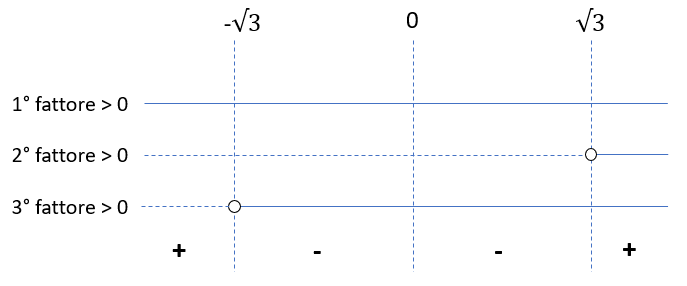
Effettuando il prodotto dei segni si ricava che la disequazione di partenza risulta verificata per
Esempio 4
Risolvere la seguente disequazione di grado superiore al secondo
Si tratta di una disequazione fratta (o frazionaria) dove al numeratore compare esplicitamente un polinomio di grado maggiore al secondo non fattorizzato.
Scomponendo il numeratore notiamo che questo può essere scritto come prodotto di polinomi e conseguentemente la disequazione assumerà la forma
A questo punto notiamo che al numeratore il termine elevato al quadrato è sempre positivo o al più nullo per x=2, mentre al denominatore il termine
non si annulla mai ed è sempre positivo.
Pertanto il segno della disequazione può essere studiato attraverso lo studio di
e
Attenzione: per x=-5 si annulla il denominatore, pertanto deve porsi x+5 maggiore e NON maggiore o uguale a zero!
Infine riportiamo le soluzioni grafiche delle ultime due disequazioni ed effettuiamo il rapporto dei segni tra numeratore e denominatore N/D, graficamente
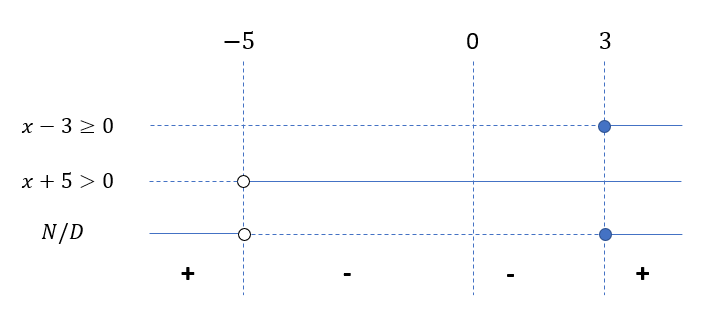
La soluzione dell’equazione di partenza è costituita dall’insieme