In matematica, la retta è uno degli argomenti fondamentali della geometria analitica. In questo articolo vedremo come riconoscerla, rappresentarla in forma analitica oltre che geometrica e scriverne l’equazione in modo chiaro e sistematico. Nei paragrafi successivi analizzeremo tutti gli aspetti principali dello studio della retta, con numerosi esempi.
Quindi niente paura, se finora rette, formule e grafici ti sono sembrati confusi, sei nel posto giusto. Ogni passaggio è costruito con logica e rigore, ma in modo chiaro e comprensibile.
Con un po’ di pratica e metodo, alla fine sarai in grado di interpretare l’equazione di una retta e risolvere gli esercizi con sicurezza, comprendendo sia il significato algebrico sia quello geometrico. Buona lettura!
Cos’è la geometria analitica
La geometria analitica è il ramo della matematica che studia le figure geometriche utilizzando strumenti algebrici. L’idea centrale è quella di associare a ogni punto del piano una coppia di valori che consentono di descrivere le entità geometriche tramite equazioni; in questo modo i problemi geometrici possono essere analizzati e risolti con metodi algebrici in modo preciso e generale.
Perché la retta è l’oggetto fondamentale in geometria analitica
La retta è il primo e più importante oggetto della geometria analitica. Si tratta di un concetto semplice dal punto di vista geometrico, ma allo stesso tempo estremamente importante dal punto di vista matematico. Attraverso lo studio delle rette si introducono infatti concetti fondamentali come coefficiente angolare, parallelismo, perpendicolarità, intersezione, e così via.
Inoltre la conoscenza della retta consente di affrontare con maggiore consapevolezza altri argomenti di matematica, non solo di geometria analitica.
Capire davvero la retta significa quindi cominciare a costruire una base solida: gran parte della geometria analitica si sviluppa infatti a partire da questo oggetto, direttamente o indirettamente.
Collegamento tra algebra, geometria analitica e il concetto di retta
In geometria analitica ogni equazione ha un significato geometrico e ogni figura può essere descritta da un’equazione. Ad esempio, nel caso della retta, questo legame è immediato: una equazione di primo grado in due incognite rappresenta infatti una retta nel piano cartesiano.
⚠️ La difficoltà principale per molti studenti non è il calcolo, ma l’interpretazione: capire cosa rappresenta un’equazione e come passare da una descrizione geometrica alla sua espressione algebrica.
Obiettivi
Al termine di questo articolo sarai in grado di:
- comprendere il significato geometrico dell’equazione della retta nella geometria analitica;
- riconoscere e utilizzare le diverse forme dell’equazione della retta;
- determinare l’equazione di una retta a partire da informazioni geometriche e/o analitiche;
- studiare la posizione reciproca di due o più rette nel piano;
- risolvere problemi geometrici utilizzando il linguaggio algebrico.
Assi cartesiani e rette parallele agli assi
Consideriamo il piano cartesiano riportato nella Fig.1:
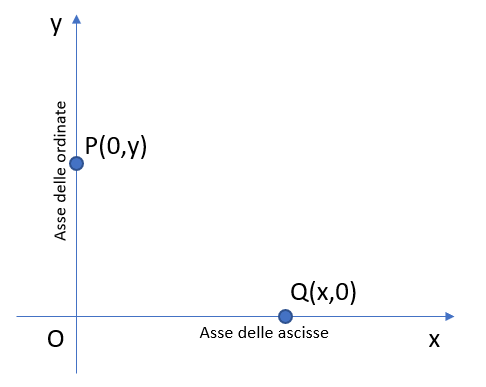
Pare abbastanza evidente che un qualunque punto che si trovi sull’asse delle ascisse abbia generiche coordinate Q(x,0), potendo pertanto concludere che tale asse è caratterizzato da tutti e soli quei punti del piano che hanno ordinata pari a zero (y=0).
Analogamente, appare del tutto evidente che l’asse delle ordinate è caratterizzato da tutti e soli i punti che hanno ascissa nulla (x=0).
Riassumendo, le equazioni degli assi cartesiani sono:
y=0 (equazione dell’asse x)
x=0 (equazione dell’asse y)
Nella Fig.2 se si considera il punto P1 sull’asse y di coordinate generiche (0,q) e si traccia una retta parallela all’asse x passante per tale punto, ci si rende facilmente conto che la retta (orizzontale in giallo) rappresenta il luogo di tutti e soli quei punti la cui ordinata è costante e pari a q. Ne consegue pertanto che un qualunque punto appartenente ad essa ha coordinate P(x,q).
Tale retta ha quindi equazione y=q.
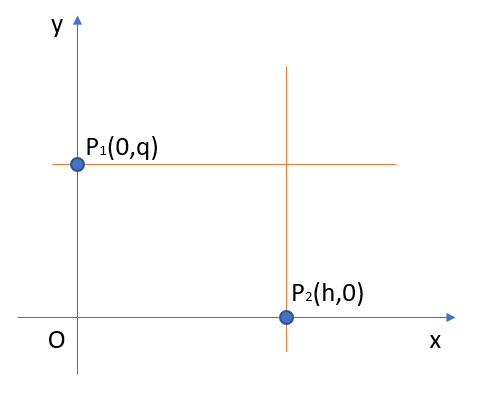
Allo stesso modo, un ragionamento analogo può essere fatto per la retta parallela all’asse y e passante per P2 di coordinate (h,0) giacente sull’asse x (retta verticale in giallo) concludendo che in geometria analitica tale retta ha equazione x=h.
Riassumendo, le equazioni delle rette parallele agli assi cartesiani sono:
y=q (equazione della retta parallela all’asse x)
x=h (equazione della retta parallela all’asse y)
Coefficiente angolare della retta e interpretazione geometrica
Definizione di coefficiente angolare
Si definisce coefficiente angolare (o parametro direttivo) di una generica retta r il parametro m tale per cui il rapporto:
è costante.
In formule:
In altre parole il coefficiente angolare di una retta generica rappresenta la variazione di ordinata per unità di variazione di ascissa.
Interpretazione geometrica del coefficiente angolare
Dal punto di vista geometrico il coefficiente angolare è direttamente legato all’inclinazione di una generica retta r rispetto al semi-asse positivo delle ascisse.
In altre parole, con riferimento alla Fig.3, il coefficiente angolare, dal punto di vista geometrico, è il rapporto tra la lunghezza dei tratti BC e CA, ma con una precisazione: i segmenti devono intendersi sempre orientati, potendo risultare il coefficiente angolare sia positivo che negativo.
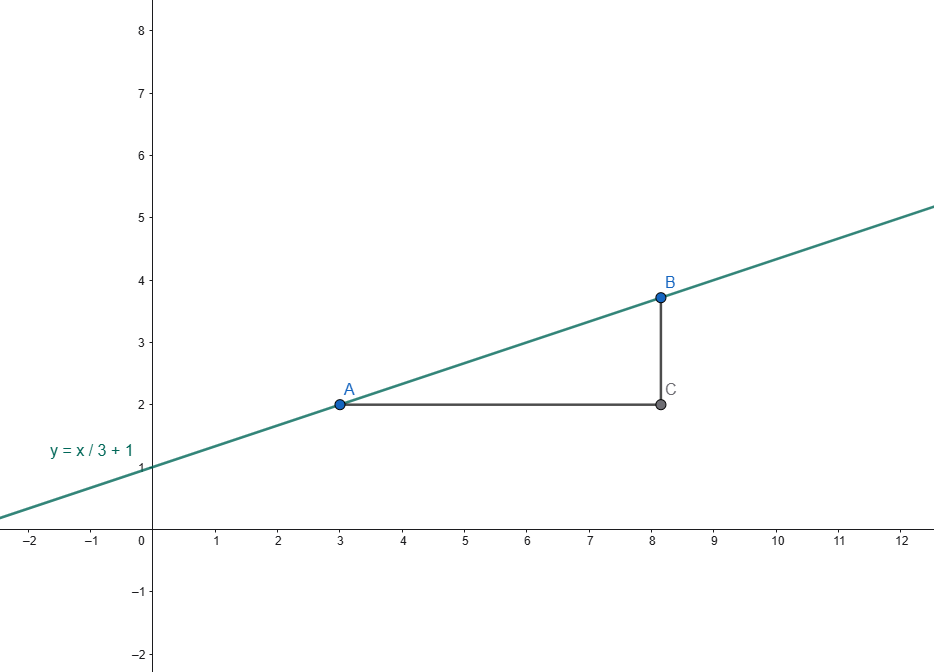
⚠️ Attenzione: non sarebbe corretto parlare di rapporto delle distanze tra i punti B e C ed i punti A e C infatti, dovendo queste risultare sempre positive, si perverrebbe ad un rapporto sempre positivo o al più nullo. Invece il coefficiente angolare può anche essere negativo.
Rette crescenti, decrescenti e orizzontali
Nel piano cartesiano una retta può avere diverse inclinazioni a seconda del valore del coefficiente angolare m, come riportato nella seguente tabella:
| m>0 | pendenza positiva (retta crescente) |
| m=0 | pendenza nulla (retta parallela all’asse x) |
| m<0 | pendenza negativa (retta decrescente) |
| m non definito | retta parallela all’asse y |
Vediamo di chiarire il tutto con degli esempi grafici ed una tabella riassuntiva prendendo a riferimento le rette riportate nella Fig.4 a seguire:
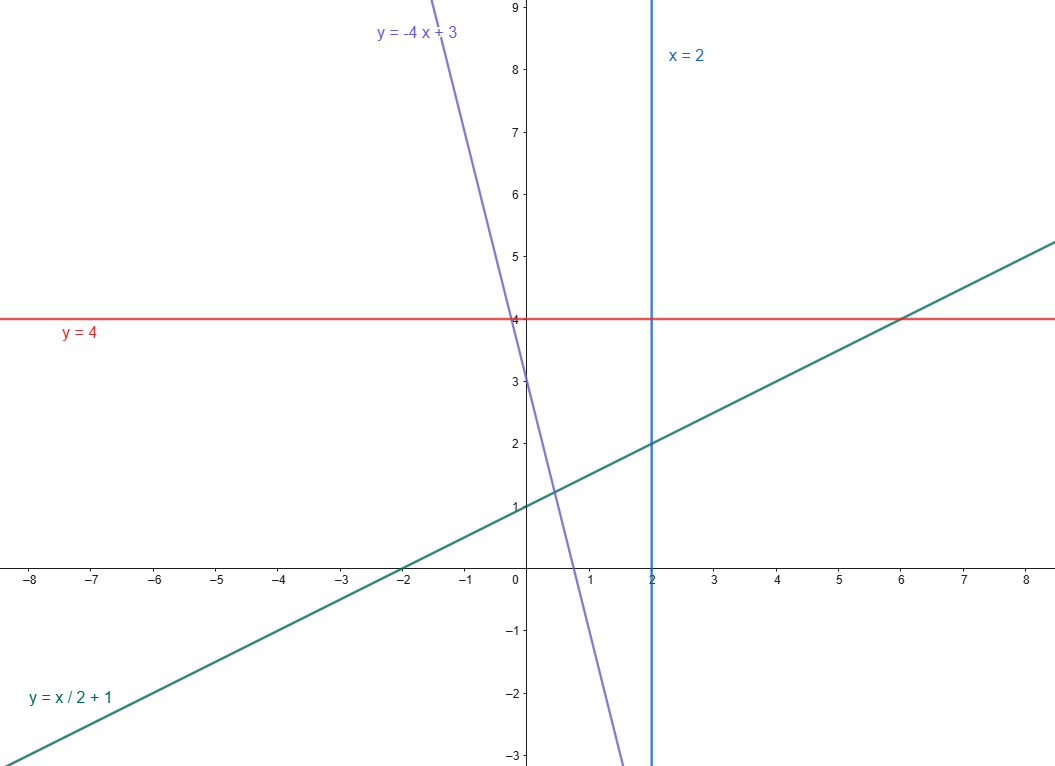
| Equazione | Coefficiente angolare m | |
| y=x/2+1 | 1/2 (m>0) | pendenza della retta positiva |
| y=4 | m=0 | pendenza della retta nulla (retta parallela all’asse x) |
| y=-4x+3 | -4 (m<0) | pendenza della retta negativa |
| x=2 | m infinito | retta parallela all’asse y |
Variazione grafica della retta al variare del coefficiente angolare
Nella figura che segue (Fig.5) viene mostrato invece come varia il grafico di una retta al variare del coefficiente angolare.
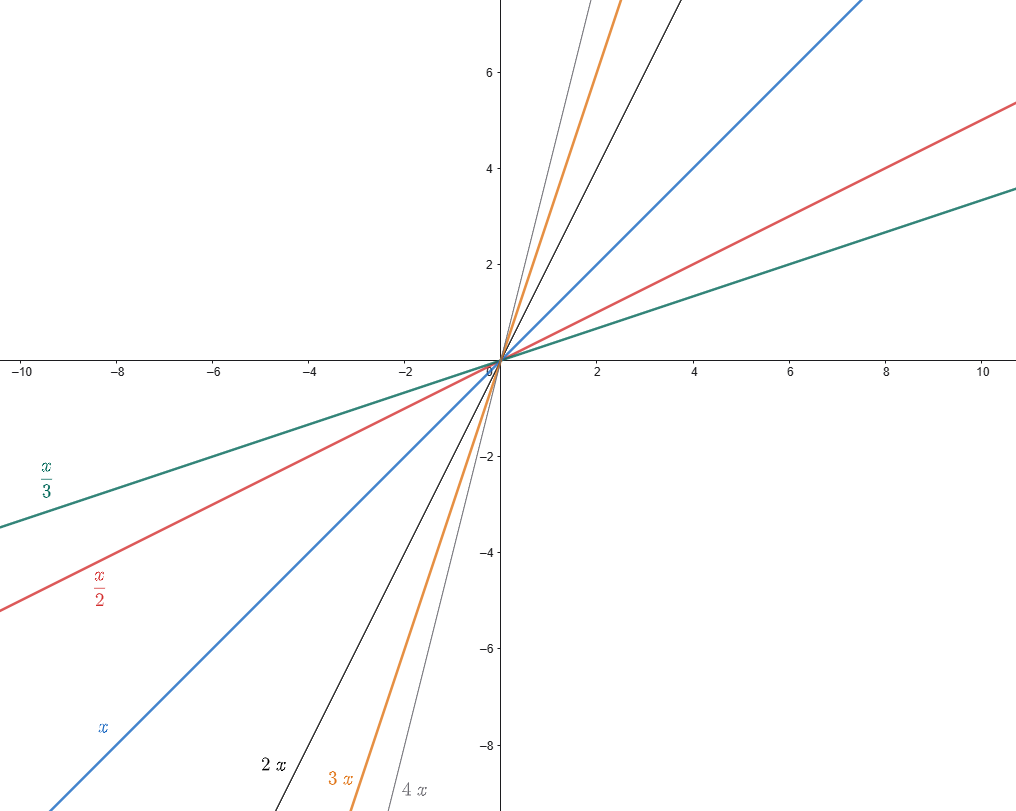
Si nota che all’aumentare del coefficiente angolare (positivi nell’esempio), aumenta anche la pendenza della retta rispetto al semiasse positivo delle ascisse. Nell’esempio in figura infatti la retta di equazione y=4x (coefficiente angolare pari a 4) è la più inclinata rispetto alle altre, mentre la meno inclinata è la retta di equazione y=x/3.
Rette particolari nel piano cartesiano
Retta passante per l’origine
Una retta passante per l’origine ha equazione del tipo:
Tale equazione rappresenta il luogo dei punti per cui l’ordinata y è proporzionale all’ascissa x secondo un coefficiente di proporzionalità costante m, che corrisponde al coefficiente angolare (o parametro direttivo).
Si nota subito che la rappresentazione fornita dalla (2) è di proporzionalità diretta. Per rendere il concetto più concreto, consideriamo un esempio pratico.
ESEMPIO
Sia m=2. L’equazione (2) diventa:
y=2x
e si ottengono per alcuni valori di x (come in tabella seguente) i corrispondenti valori di y. Si nota subito che i valori trovati esprimono proporzionalità diretta e che il coefficiente di proporzionalità è proprio il coefficiente angolare.
| x | -1 | 0 | 1 | 2 | 3 |
| y | -2 | 0 | 2 | 4 | 6 |
Equazioni della retta in geometria analitica
Forma esplicita dell’equazione della retta
L’equazione della retta in forma esplicita può scriversi come:
dove è il coefficiente angolare e \(q\) l’ordinata all’origine.
Tale forma viene chiamata anche equazione della funzione lineare (funzione intera razionale algebrica di 1° grado).
Equazione generale della retta
Una retta qualunque, nel piano, può essere rappresentata nel caso più generale, al variare dei coefficienti reali a, b e c dalla seguente equazione:
La (4) prende il nome di equazione generale della retta oppure di equazione della retta in forma implicita, ove con \(c\) si è indicato il termine noto.
Verifichiamo adesso che ogni equazione di questo tipo rappresenta una retta.
Effettuiamo in particolare la seguente ipotesi iniziale:
In questo caso l’equazione generale (4) può essere messa nella forma:
che rappresenta l’equazione di una retta generica di coefficiente angolare pari a:
ed ordinata all’origine pari a:
Dal punto di vista geometrico l’equazione (5) rappresenta una generica retta del piano non passante per l’origine e non parallela ad alcuno degli assi coordinati.
Rette parallele e rette perpendicolari
Condizione di parallelismo
In geometria analitica, due rette (non parallele all’asse delle ordinate) si dicono parallele (tra loro) se hanno lo stesso coefficiente angolare. Analogamente, se due rette hanno il medesimo coefficiente angolare, esse sono certamente parallele, in formule si ha:
Ricordiamo che per i casi di rette parallele all’asse x, queste hanno coefficiente angolare nullo; per le rette parallele all’asse delle ordinate il coefficiente angolare invece non è definito.
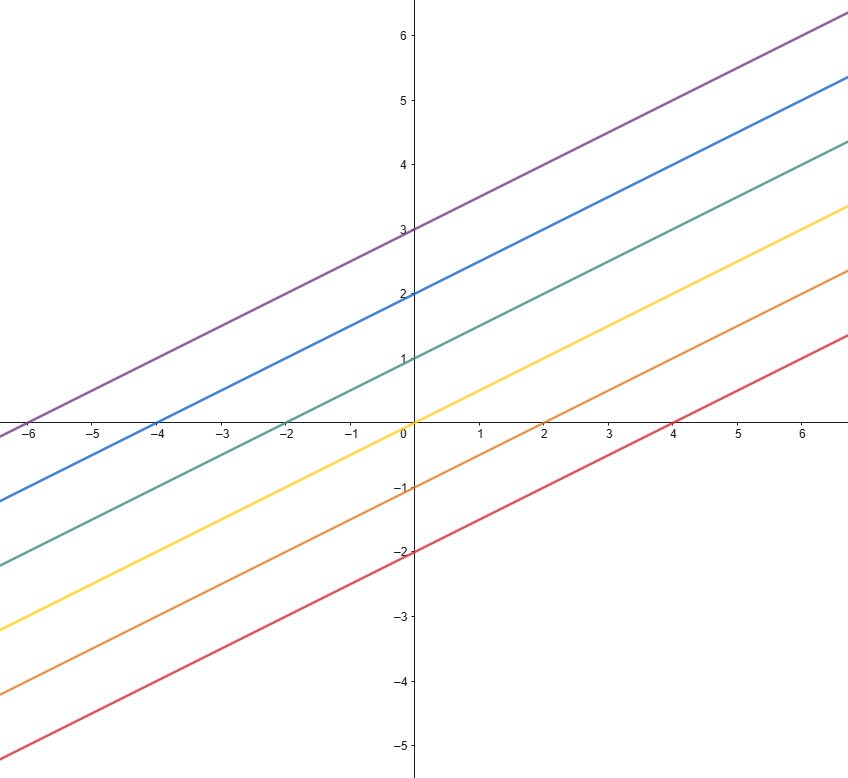
ESEMPIO GRAFICO di rette parallele (coefficiente angolare m=1/2)
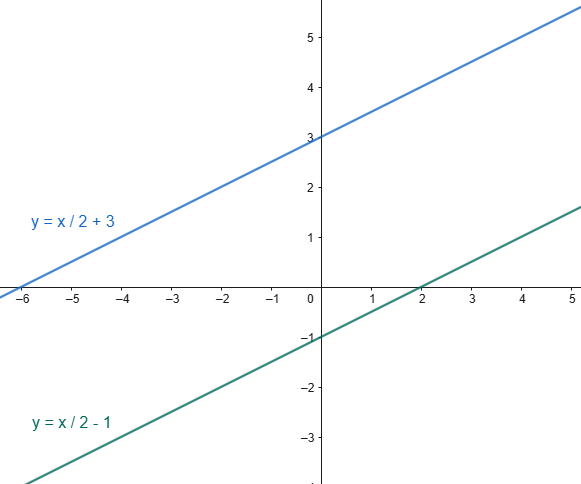
Si nota molto chiaramente come le rette rappresentate nella figura qui in alto (Fig.6) sono parallele tra loro ed hanno il medesimo coefficiente angolare 1/2.
Condizione di perpendicolarità
Analogamente al caso visto in precedenza sul parallelismo di rette, è possibile definite analiticamente una condizione tale per cui due rette sono perpendicolari tra loro. Si precisa che la formale dimostrazione della perpendicolarità tra due rette verrà trattata in uno specifico articolo in quanto, al momento, ciò che ci interessa è il risultato concettuale matematico e l’applicazione pratica (essere in grado di saper risolvere gli esercizi).
Ciò premesso, diremo che due rette, non parallele agli assi, sono ortogonali tra loro se il prodotto del loro coefficiente angolare è pari a -1 (può anche dirsi, in maniera del tutto equivalente, che i coefficienti angolari sono l’uno l’opposto del reciproco dell’altro). Quanto appena enunciato rappresenta inoltre una condizione necessaria e sufficiente.
In formule si ha:
oppure, il che è lo stesso:
Notiamo infine che se una delle due rette è parallela all’asse delle x (per esempio la retta s), questa avrà certamente coefficiente angolare nullo (ms=0), mentre la retta r avrà coefficiente angolare infinito.
ESEMPIO GRAFICO di rette ortogonali (coefficiente angolare ms=4 e mr=-1/4)
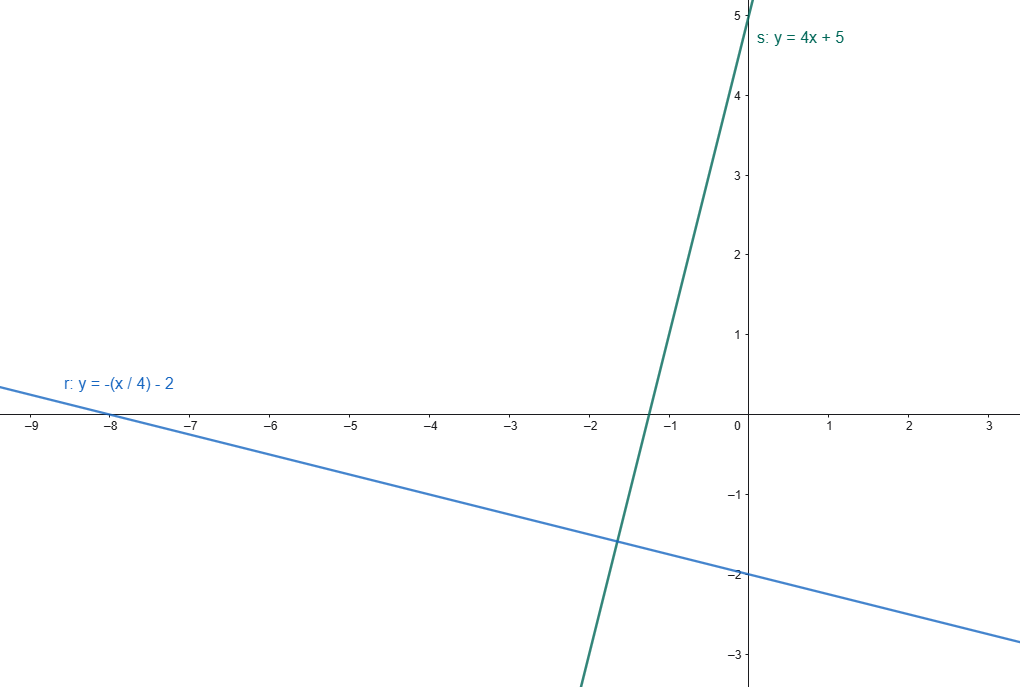
Equazioni fondamentali della retta
Equazione della retta passante per un punto e con coefficiente angolare assegnato
L’equazione della retta passante per un punto e con coefficiente angolare noto può ricavarsi immediatamente dall’equazione del fascio proprio; basterà infatti imporre un certo valore del coefficiente angolare per ottenere la retta desiderata.
L’equazione della retta in tal caso assume la seguente forma:
con coefficiente angolare \(m\) noto.
ESEMPIO
Si vuole determinare l’equazione della retta r di coefficiente angolare m=-2 e passante per il punto P0 di coordinate P0=(4,3).
In tal caso scriveremo, dopo aver effettuato le dovute sostituzioni:
ed ancora, semplificando:
che rappresenta l’equazione della retta ricercata.
Coefficiente angolare della retta passante per due punti
Si considerino i punti P e Q rispettivamente di coordinate P(x1,y1) e Q(x2,y2) tali che la retta r per PQ sia non parallela all’asse delle ordinate.
Si definisce coefficiente angolare di r il rapporto tra la differenza di ordinate e la differenza di ascisse tra i due punti, come da diretta applicazione della (1); in formule si ha:
Note:
- nella scrittura di tale ultima espressione di \(m\) i punti P e Q sono intercambiabili, infatti può anche scriversi, senza alterare il significato che:
- il coefficiente angolare \(m\) può essere ricavato a partire dalla sola conoscenza dei due punti P e Q, senza tuttavia scrivere l’equazione della retta passante per tali punti.
ESEMPIO
Si vuole determinare il coefficiente angolare della retta passante per i punti di coordinate A(2,3) e B(-2,6).
Applicando la (7) per il calcolo di \(m\) si ottiene:
Equazione della retta passante per due punti
In questo paragrafo vediamo come scrivere correttamente l’equazione di una retta passante per due punti noti P e Q.
In particolare, noti che siano due punti del piano cartesiano di coordinare P(x1,y1) e Q(x2,y2) scelti in modo tale che la retta passante per questi punti non sia parallela né all’asse x, né all’asse y, è possibile dimostrare che la retta passante per tali punti può scriversi come:
ESEMPIO
Determinare l’equazione della retta passante per i punti di coordinate P(3,6) e Q(-10,-1).
Utilizzando la formula (8), possiamo scrivere:
da cui
quindi semplificando
che rappresenta l’equazione della retta (scritta in forma implicita) passante per i punti P e Q.
Per un approfondimento completo con esempi svolti passo passo e casi particolari, si rimanda all’articolo dedicato al calcolo dell’equazione della retta passante per due punti.
Equazione segmentaria della retta
Caso particolare, ricavabile direttamente dell’equazione della retta per due punti (8), è quello in cui i punti appartengono agli assi cartesiani, quindi un punto appartiene all’asse delle ascisse, l’altro a quello delle ordinate.
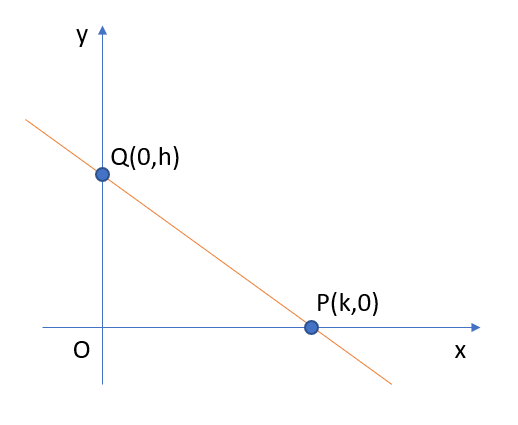
Per esempio, immaginiamo che P appartenga all’asse delle ascisse: in tal caso le sue coordinate generiche possono scriversi come P(k,0); allo stesso modo ipotizziamo che il punto Q sull’asse delle ordinate avrà coordinate generiche Q(0,h).
Sostituendo tali coordinate all’equazione (8), questa può scriversi come:
da cui si ricava immediatamente, dopo aver distribuito il denominatore a secondo membro e riordinando:
che rappresenta l’equazione segmentaria della retta.
Distanza di un punto da una retta
Capita spesso in molte applicazioni della geometria di dover calcolare la distanza di un punto P(x0,y0) rispetto ad una retta r nota. Tale distanza è da intendersi come distanza minima di P da r.
In particolare, si può dimostrare, rimandando la dimostrazione completa ad un articolo dedicato, che tale distanza si può esprimere come:
con r di equazione
Nota: si può dimostrare che il segmento rappresentativo della minima distanza tra P ed r interseca ortogonalmente tale retta.
Per comprenderne meglio tali concetti analizziamone il significato geometrico con un semplice esempio svolto.
ESEMPIO DI CALCOLO DI DISTANZA DI UN PUNTO DA UNA RETTA
Calcolare la distanza del punto P dalla retta r.
Dati:
P(8,5) -> x0=8; y0=5
r: x+2y+2=0 -> a=1, b=2, c=2
Per comprenderne meglio il significato geometrico, mostriamo il risultato in un piano cartesiano (Fig.9):
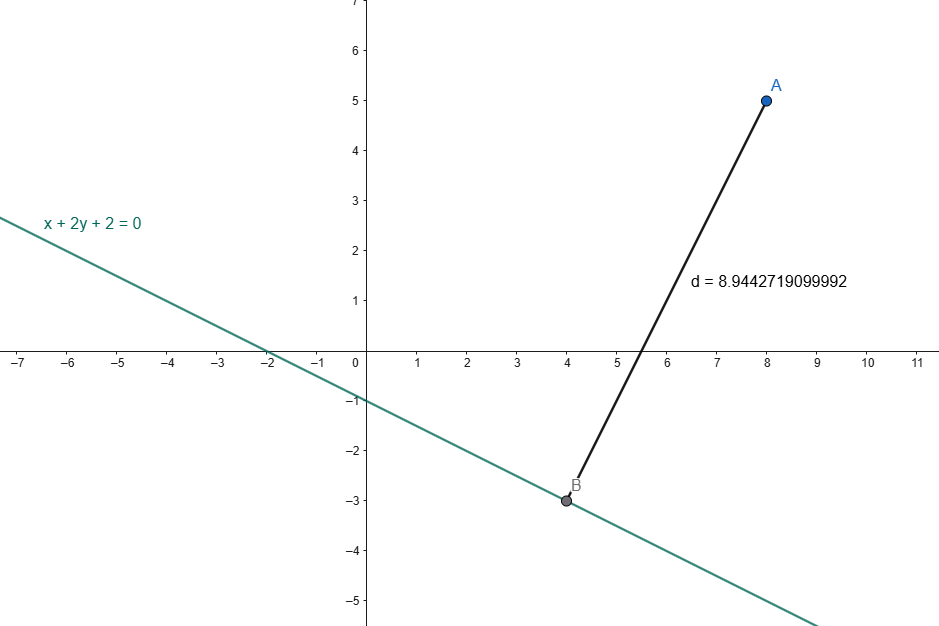
Si nota che nel caso di distanza di una retta r dall’origine O, la formula (10) vista sopra per il calcolo della distanza si riduce a:
poiché risulta evidentemente x0=y0=0.
Fasci di rette in geometria analitica
Fascio improprio di rette
In geometria analitica per fascio improprio di rette ci si riferisce all’insieme delle rette del piano aventi tutte la stessa direzione. Tali rette sono pertanto tutte quante parallele tra loro e, conseguentemente, hanno tutte il medesimo coefficiente angolare m.
Diremo quindi che, con m costante, al variare del parametro k, la generica equazione del fascio improprio di rette si esprime come:
Notiamo inoltre che per k=0, si ottiene l’equazione del fascio improprio passante per l’origine: tale retta prende il nome di retta base del fascio alla quale tutte le altre sono parallele al variare di k.
⚠️ L’equazione sopra esposta non è utilizzabile per la rappresentazione del fascio improprio di rette parallele all’asse y (poiché m, in tal caso, non è definito).
In tale particolare caso, per descrivere il fascio improprio di rette parallele all’asse y, vale l’equazione:
Fascio proprio di rette
In geometria analitica il fascio proprio di rette è costituito dall’insieme di rette del piano cartesiano passanti per uno stesso punto detto centro del fascio al variare del coefficiente angolare \(m\).
Nella Fig.11 possiamo osservare, a titolo di esempio, l’insieme di alcune rette passanti per il punto di coordinate C=(2,3) che rappresenta il centro del fascio.
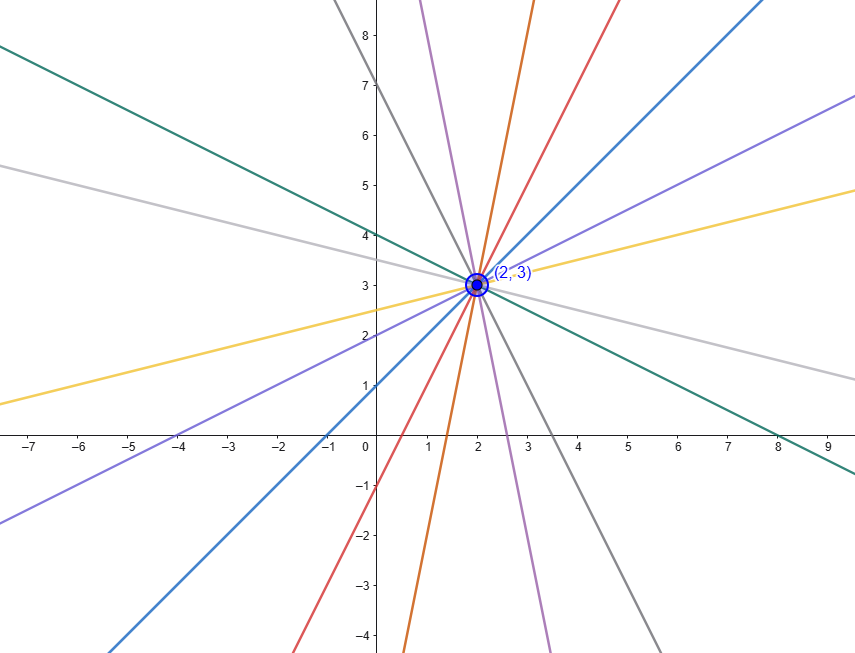
In generale, per poter esprimere analiticamente l’equazione di una qualsiasi retta passante per il centro del fascio C di coordinate C=(x0,y0) note, è possibile ricorrere alla seguente formulazione:
al variare del coefficiente angolare m.
⚠️ Notiamo che l’espressione (13) non può essere utilizzata per descrivere la retta parallela all’asse y non essendo definito, in questo caso, il coefficiente angolare.
Luoghi geometrici nel piano cartesiano
Definizione di luogo geometrico
I luoghi geometrici rappresentano uno dei concetti fondamentali della geometria e costituiscono un ponte tra le proprietà dei punti e le figure geometriche che ne derivano. Attraverso questa idea è possibile descrivere rette, curve e superfici non solo come disegni, ma come insiemi di punti che soddisfano precise condizioni geometriche. Comprendere cosa sia un luogo geometrico permette di affrontare in modo più consapevole lo studio di figure come la retta (ma non solo), e di sviluppare un metodo rigoroso per risolvere problemi geometrici. In questo paragrafo vedremo che cosa si intende per luogo geometrico, come riconoscerlo e perché è uno strumento così importante nello studio della matematica.
Un luogo geometrico è l’insieme di tutti e soli i punti del piano (o dello spazio) che soddisfano una determinata condizione geometrica.
In altre parole:
- ogni punto che rispetta la condizione appartiene al luogo geometrico;
- nessun punto che non la rispetta ne fa parte.
Per esempio la circonferenza è il luogo geometrico dei punti del piano che hanno distanza costante da un punto fisso detto centro.
Questa definizione è fondamentale nello studio della geometria perché permette di descrivere figure geometriche tramite proprietà comuni.
Il concetto di luogo geometrico si applica anche alle rette.
In geometria analitica una retta può infatti essere vista come un luogo geometrico, perché è l’insieme di tutti i punti che soddisfano una certa condizione.
Esempi
- La retta per due punti è il luogo geometrico dei punti allineati con due punti dati.
- L’asse di un segmento è il luogo geometrico dei punti che hanno uguale distanza dagli estremi del segmento.
- La retta parallela a una retta data e passante per un punto è il luogo geometrico dei punti che mantengono una specifica relazione di parallelismo.
Quindi rette, curve e superfici in generale possono tutte essere interpretate come luoghi geometrici, purché siano definite tramite una proprietà comune dei loro punti.
A seguire, in particolare faremo riferimento a due specifiche tipologie di luoghi geometrici:
- l’asse di un segmento;
- la bisettrice di un angolo.
Asse di un segmento
L’asse di un segmento, come già accennato, può essere definito come il luogo dei punti equidistanti dagli estremi del segmento.
Con riferimento alla Fig.12 si immagini di voler determinare l’equazione dell’asse del segmento AB applicando la definizione di luogo geometrico.
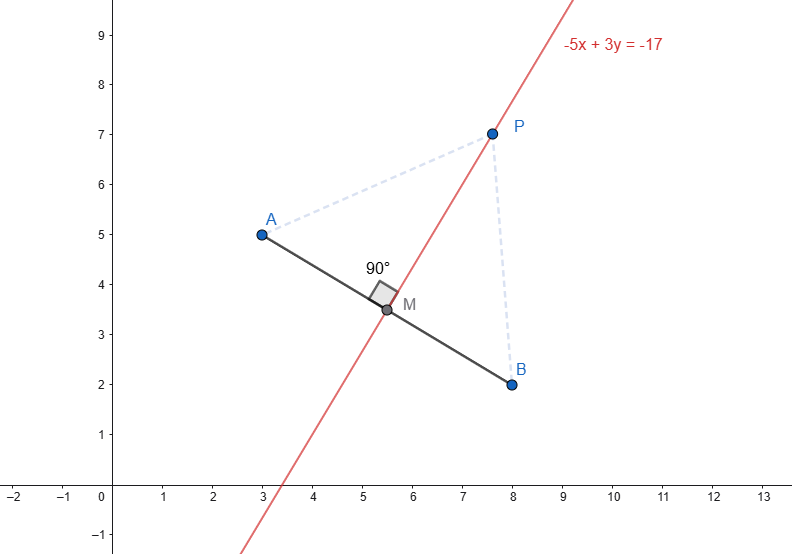
In particolare sono note le coordinate dei punti A e B, che valgono rispettivamente
A(3,5)
B(8,2)
L’equazione dell’asse del segmento AB può ottenersi imponendo che questo sia il luogo dei punti tali per cui la misura del segmento AP è uguale alla misura del segmento BP, essendo P un generico punto di coordinare P(x,y), in formule:
e quindi, applicando la formula per il calcolo della distanza tra due punti, si ha, in generale:
Nel caso in esame può quindi scriversi:
che semplificata diventa, dopo aver svolto i vari passaggi:
L’equazione finale semplificata è quella di una retta, luogo geometrico dei punti equidistanti dai punti:
A=(3,5) e B=(8,2).
Bisettrice di un angolo
In questo paragrafo ci occuperemo di determinare un altro luogo geometrico molto noto, in particolare quello che rappresenta le bisettrici degli angoli formati da due rette incidenti.
Immaginiamo di avere due rette r ed s non parallele tra loro di equazioni
r: ax+by+c=0
s: a’x+b’y+c’=0
Sappiamo che la bisettrice di un angolo è costituita dal luogo dei punti equidistanti dalle rette r ed s, pertanto se si indica con P(x,y) un generico punto appartenente alla bisettrice si può certamente scrivere che:
La (15) consente di determinare le equazioni delle bisettrici di un angolo. Vediamolo con un esempio pratico.
ESEMPIO
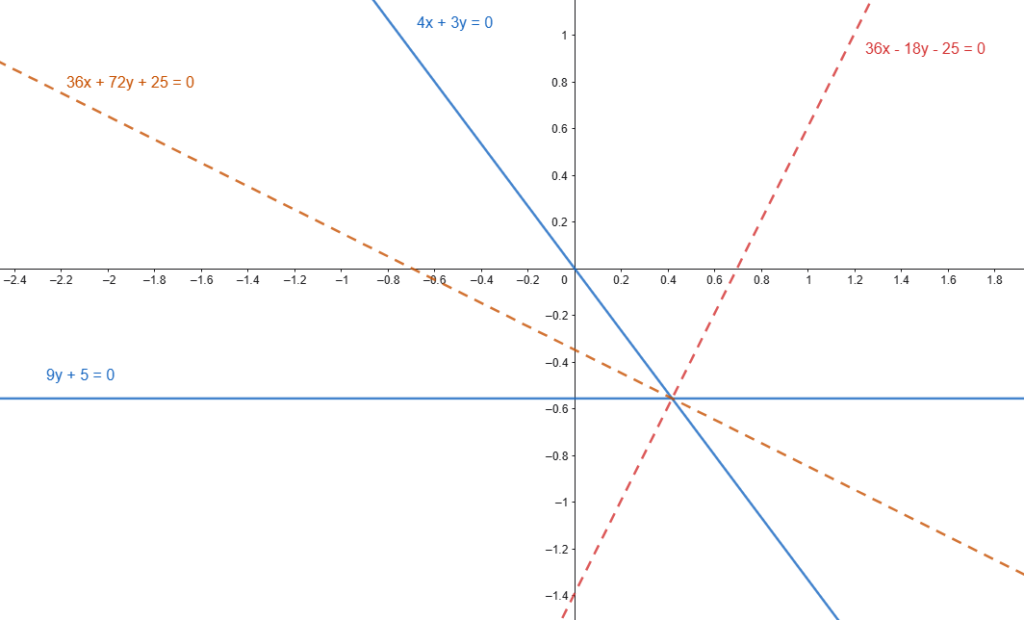
Date le equazioni
r: 4x+3y=0
s: 9y+5=0
si determinino le equazioni delle bisettrici degli angoli formati dalle medesime rette r ed s.
Soluzione:
Applicando la (15) si ottiene:
da cui
quindi ancora
Semplificando si ottengono le equazioni delle due bisettrici:
Equazioni parametriche di un luogo
Un altro modo per ricavare l’equazione di un luogo geometrico è quello delle equazioni parametriche.
Un sistema di equazioni parametriche può scriversi in generale nella forma:
Per ottenere l’equazione del luogo in forma cartesiana si procede ad eliminare il parametro t dal sistema.
ESEMPIO
Determinare l’equazione cartesiana del seguente luogo geometrico:
Soluzione
Isoliamo t dalla prima equazione
ottenendo così l’equazione della retta in forma cartesiana esplicita.
⚠️ Attenzione:
- Non tutte le rette possono essere scritte in forma esplicita (ad esempio le rette verticali \(x=k\).
- Tutte le rette possono invece essere scritte in forma implicita.
Conclusione
La retta rappresenta uno degli elementi fondamentali della geometria analitica e costituisce la base per lo studio degli argomenti successivi (es: parabola, circonferenza, ellisse, iperbole, etc.).
Attraverso le diverse rappresentazioni – esplicita, implicita e parametrica – abbiamo visto come sia possibile descrivere in modo preciso ed analitico ogni retta, determinare quelle passanti per due punti dati e identificare rette parallele o perpendicolari a una retta nota, ma non solo!
La retta è inoltre un luogo geometrico, un insieme di punti che soddisfano una relazione lineare, e costituisce il punto di partenza per affrontare concetti più complessi (es: bisettrici).
La comprensione della retta è essenziale anche per collegarsi ad altri argomenti di geometria analitica, come lo studio di luoghi geometrici più complessi, le intersezioni tra rette e curve, l’estensione delle rette nello spazio tridimensionale e le trasformazioni geometriche come traslazioni e rotazioni. In sintesi, conoscere bene la retta permette di affrontare con sicurezza e metodo tutti i successivi approfondimenti della geometria analitica e gli ulteriori argomenti correlati di cui la retta è elemento imprescindibile.