Le disequazioni di secondo grado sono un argomento fondamentale della matematica delle scuole superiori. Imparare a risolverle è essenziale per affrontare problemi più complessi e sviluppare capacità logiche. In questo articolo vedremo cos’è una disequazione di secondo grado, i passaggi per risolverla e ben 5 esempi svolti passo passo.
Cosa sono le Disequazioni di Secondo Grado?
Una disequazione di secondo grado assume una forma generale del tipo:
oppure
dove:
- a,b,c sono numeri reali,
- a≠0.
L’obiettivo è trovare l’insieme delle soluzioni per cui l’espressione è maggiore o minore di zero.
In altre parole bisogna studiare il segno del trinomio di secondo grado associato alla disequazione stessa.
Come si Risolve una Disequazione di Secondo Grado
Per risolvere una disequazione di secondo grado, segui questi passaggi:
1. Calcola il discriminate (delta)
2. Determina le radici dell’equazione associata
3. Studia il segno del trinomio usando:
- Il grafico della parabola,
- Una tabella dei segni.
4. Individua l’intervallo di soluzioni coerente con la disequazione (>, ≥, <, ≤).
SIAMO ANCHE SU YOU TUBE
Disequazioni di Secondo Grado: come risolverle + ESERCIZI SVOLTI | video tutorial con spiegazione
Hai difficoltà con le disequazioni di secondo grado? In questo video ti spiego passo dopo passo come risolverle in modo chiaro e veloce! 🔥
📘 Cosa imparerai:
- Come si riconosce una disequazione di secondo grado
- La forma canonica
- Come calcolare il discriminante Δ e interpretarlo
- I casi principali:
- Δ maggiore di 0 → due soluzioni reali
- Δ uguale a 0 → una sola soluzione (doppia)
- Δ minore di 0 → nessuna soluzione reale
- Come determinare l’intervallo delle soluzioni in base al segno di 𝑎.
- Come rappresentare graficamente la parabola e leggere le soluzioni sul piano cartesiano.
- Esempi svolti con frazioni e radicali, per imparare a gestire anche i casi più complessi!
Argomenti trattati nel video
CAPITOLI
00:00 Introduzione
01:54 Delta maggiore di 0
03:52 Delta uguale a 0
05:05 Delta minore di 0
05:29 Casi particolari (disequazioni pure e spurie)
08:34 Esercizi Svolti (passo passo)
18:34 Esercizi da svolgere e conclusioni
🔔 Resta aggiornato! VISITA IL NOSTRO CANALE YOU TUBE e non dimenticare di ISCRIVERTI 🙂
Esempi svolti di Disequazioni di Secondo Grado
ESEMPIO N.1
Risolvere la seguente disequazione di secondo grado:
Calcoliamo il discriminante:
Le radici dell’equazione associata valgono: x1=2, x2=3.
Dallo studio del segno del trinomio di secondo grado risulta che il segno del primo coefficiente è positivo (a=1>0), mentre il verso della disequazione è anch’esso positivo. Possiamo concludere che le soluzioni della disequazione sono esterne all’intervallo aperto (2,3), graficamente:
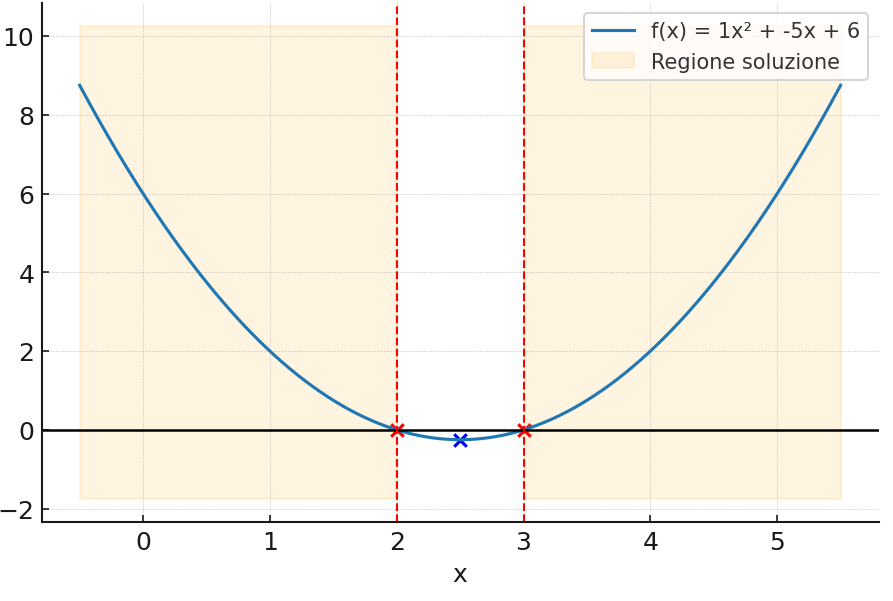
alternativamente la soluzione della disequazione può essere disegnata utilizzando un grafico come questo:

ESEMPIO N.2
Risolvere la seguente disequazione di secondo grado:
Calcoliamo il discriminante:
Le radici dell’equazione associata valgono: x1=1, x2=3.
Dallo studio del segno del trinomio di secondo grado risulta che il segno del primo coefficiente è positivo (a=2>0), mentre il verso della disequazione è negativo. Possiamo concludere che le soluzioni della disequazione sono interne all’intervallo chiuso [1,3]
Soluzione: 1≤x≤3, graficamente:
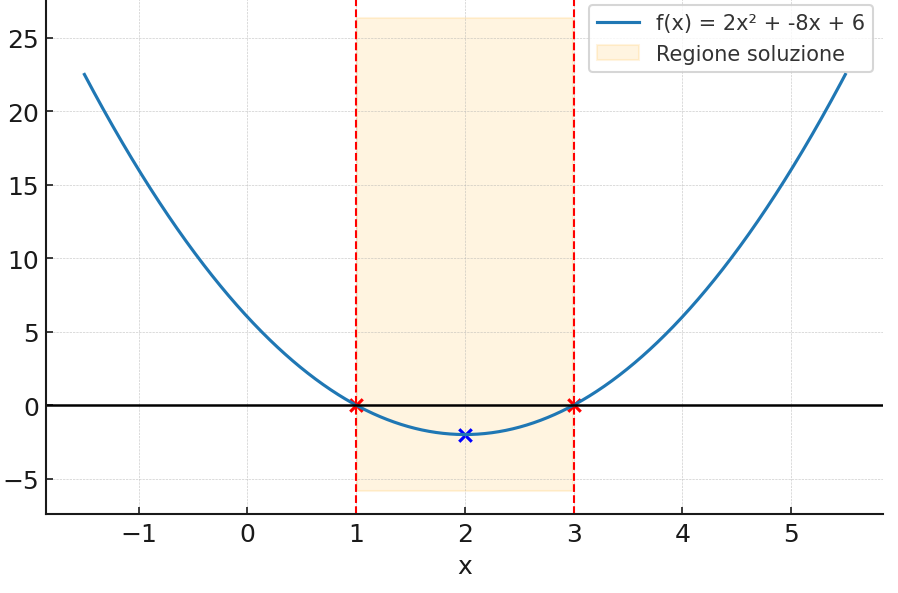
alternativamente la soluzione della disequazione può essere disegnata utilizzando un grafico come questo:

ESEMPIO N.3
Risolvere la seguente disequazione di secondo grado:
Se proviamo a calcolare il discriminante otteniamo:
che essendo minore di zero implica l’inesistenza di soluzioni (dell’equazione associata!) appartenenti al campo dei numeri reali.
Conseguentemente le soluzioni della disequazione non potranno che essere, in questo caso, o tutte positive o tutte negative.
Dallo studio del segno del trinomio di secondo grado risulta che il segno del primo coefficiente è positivo (a=1>0), mentre il verso della disequazione è negativo. Possiamo concludere che non vi sono soluzioni che verificano la disequazione data, in altre parole la soluzione è rappresentata dall’insieme vuoto.
Graficamente:
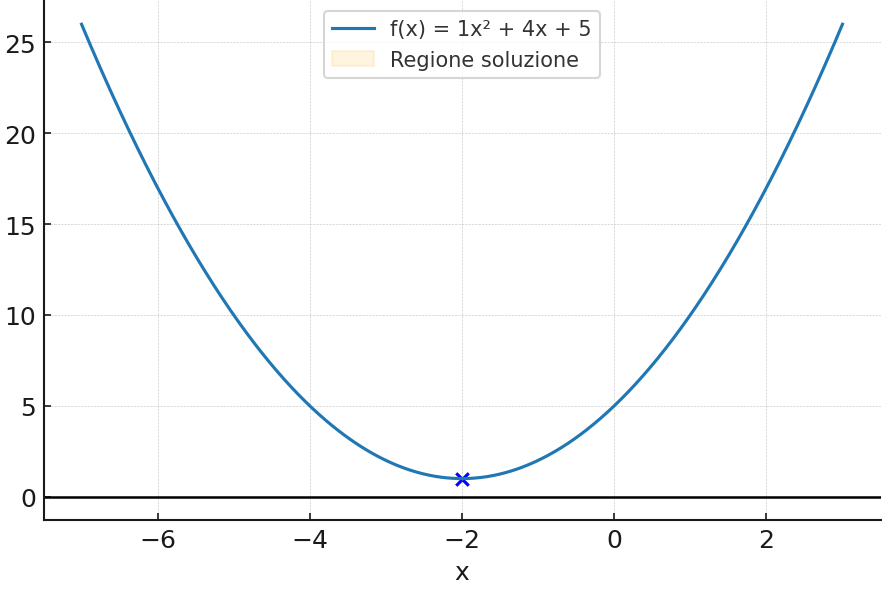
ESEMPIO N.4
Risolvere la seguente disequazione di secondo grado:
Calcoliamo il discriminante:
Le radici dell’equazione associata valgono: x1=-1, x2=4.
Dallo studio del segno del trinomio di secondo grado risulta che il segno del primo coefficiente è negativo (a=-1<0), mentre il verso della disequazione è maggiore o uguale a zero. Possiamo concludere che le soluzioni della disequazione sono interne all’intervallo chiuso -1≤x≤4, graficamente:
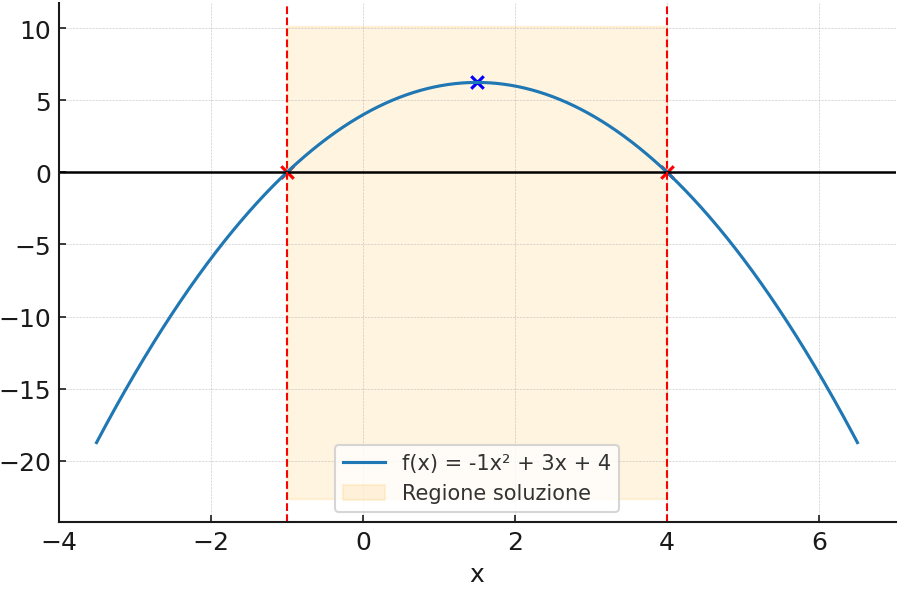
in alternativa la soluzione della disequazione può essere disegnata utilizzando un grafico come questo:

ESEMPIO N.5
Risolvere la seguente disequazione di secondo grado:
L’equazione associata alla disequazione è
da cui si ottengono subito le soluzioni: x1=-3, x2=3.
Dallo studio del segno del binomio associato alla disequazione risulta che il segno del primo coefficiente è positivo (a=1>0), mentre il verso della disequazione è maggiore o uguale a zero. Possiamo concludere che le soluzioni della disequazione sono esterne all’intervallo compreso tra le radici:
Soluzione:
graficamente:
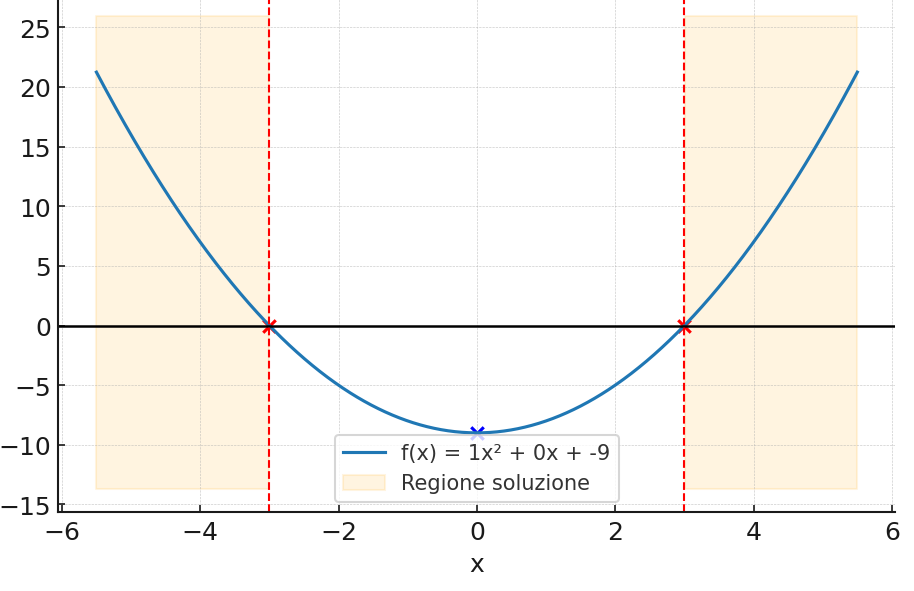
in alternativa la soluzione della disequazione può essere disegnata utilizzando un grafico come questo:

Consigli per Studiare le Disequazioni di Secondo Grado
- Memorizza bene la forma generale e il ruolo del discriminante.
- Usa strumenti come la tabella dei segni oppure puoi studiare il segno del trinomio di secondo grado associato alla disequazione: è lo strumento più rapido per capire dove il trinomio è positivo o negativo!
- Allenati con tanti esercizi per acquisire padronanza e velocità (aspetto fondamentale!).
Disequazioni di secondo grado PDF da scaricare
Ti lascio un link di seguito in cui potrai trovare tanti esercizi svolti in formato pdf per esercitarti e migliorare le competenze con le disequazioni di secondo grado
Conclusione
Le disequazioni di secondo grado sono uno strumento fondamentale in matematica. Una volta capita la logica, risolverle diventa meccanico: basta calcolare il discriminante, trovare le radici e studiare il segno della parabola.
Con i 5 esempi svolti che abbiamo visto insieme ora dovresti avere una base più solida per affrontare gli esercizi.
Se hai dubbi sull’argomento, scrivici pure alla sezione il prof risponde.
Alla prossima!

