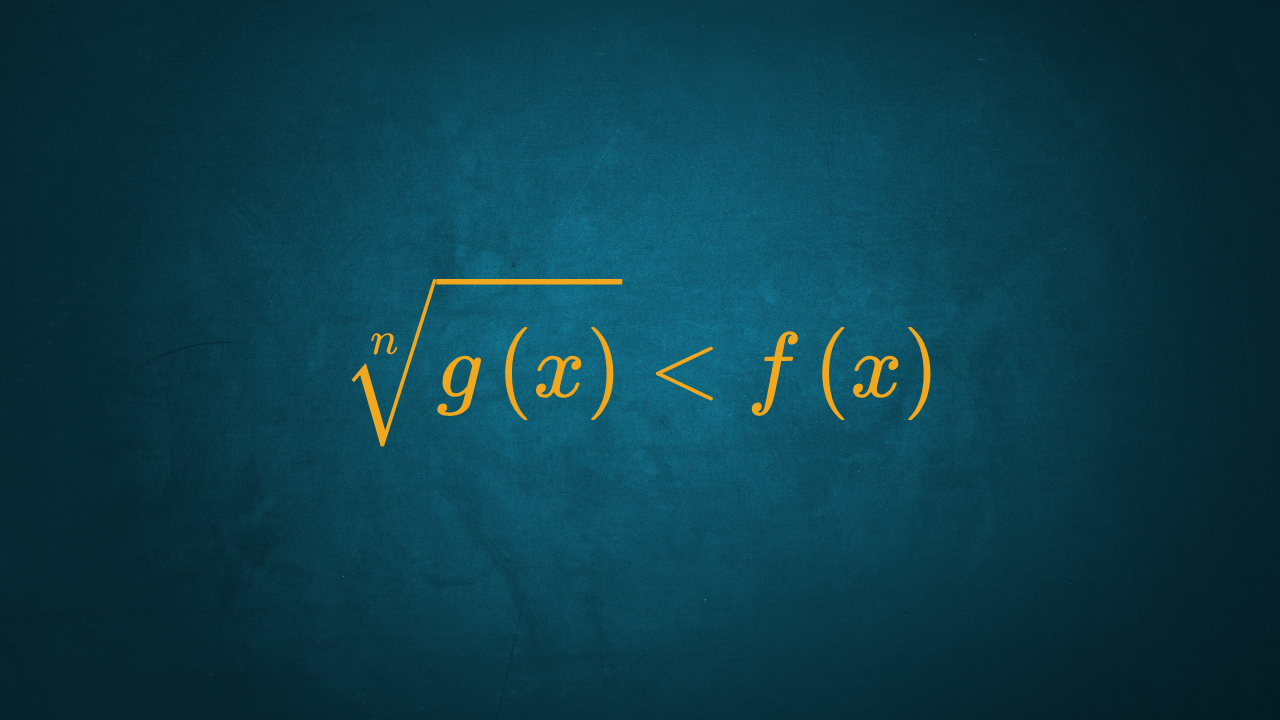Le disequazioni irrazionali sono un tipo di disequazioni in cui l’incognita compare all’interno di una radice quadrata, cubica o di altro indice.
Sono molto comuni nei problemi di algebra e analisi, e rappresentano un passaggio fondamentale nello studio delle equazioni e disequazioni di secondo grado.
Risolvere una disequazione irrazionale significa trovare i valori dell’incognita che rendono vera l’espressione, tenendo conto che, a causa delle radici, il dominio (cioè l’insieme dei valori ammessi) gioca un ruolo cruciale.
In questa guida imparerai passo per passo:
- cos’è una disequazione irrazionale e come riconoscerla;
- le tecniche principali di risoluzione;
- esempi pratici di difficoltà crescente;
- gli errori più comuni da evitare;
- un riepilogo con esercizi e soluzioni.
La spiegazione completa è disponibile anche in formato video.
Videolezione su “Disequazioni Irrazionali | Guida completa + Esercizi passo passo”
Il video propone una guida completa alle disequazioni irrazionali, adatta sia a studenti delle scuole superiori sia universitari.
La spiegazione include teoria, esempi pratici ed esercizi svolti passo passo, con un approccio sistematico e rigoroso.
Argomenti trattati nel video
00:00 Introduzione alle disequazioni irrazionali
00:53 Esempi, forme e dominio
03:28 Come risolvere una disequazione irrazionale (teoria completa)
07:36 Esercizio svolto N.1
11:25 Esercizio svolto N.2
12:03 Esercizio svolto N.3
15:41 Esercizio svolto N.4
19:16 Esercizio svolto N.5
22:46 Esercizio svolto N.6
25:16 Esercizio svolto N.7
28:38 Esercizio svolto N.8
31:10 Esercizi aggiuntivi con soluzione
Per altri contenuti di matematica, è possibile seguire anche il canale YouTube.
Cos’è una disequazione irrazionale
Una disequazione irrazionale è una disuguaglianza che contiene l’incognita sotto il segno di radice.
Esempio tipico:
oppure
In generale, la forma può essere ricondotta ad una delle seguenti tipologie:
Il dominio: il primo passo fondamentale
Prima di qualsiasi manipolazione, bisogna individuare il dominio della disequazione, ossia l’insieme dei valori per cui tutte le radici hanno senso.
Ad esempio, nella disequazione:
possiamo calcolare il dominio imponendo che il radicando sia non negativo:
Solo questi valori sono ammessi: per tutti gli altri la radice non è definita nei numeri reali.
⚠️ Errore comune: dimenticare di imporre il dominio porta a soluzioni “false” che non esistono realmente.
Strategie generali di risoluzione delle disequazioni irrazionali
Le strategie cambiano in base al tipo di radice e alla posizione dell’incognita.
Vediamo di seguito i principali due casi risolutivi, nella maggior parte dei casi infatti tutti gli altri sono riconducibili ad essi.
1° Caso – La disequazione irrazionale si trova nella forma
dove f(x) e g(x) sono espressioni contenenti la x.
Notiamo che, se n è pari, la radice esiste solo se
ed il radicale ha valore positivo o al più nullo.
Invece se n è dispari per risolvere la disequazione irrazionale basterà elevare primo e secondo membro alla potenza n-esima e risolvere la disequazione ottenuta in maniera del tutto equivalente
Riassumendo, per n dispari, si ha
| \[f(x)>\sqrt[n]{g(x)}\rightarrow\left[f(x)\right]^n>g(x)\] | se n dispari |
Se invece n è pari, come già anticipato, dovrà risultare g(x) positiva o al più nulla (affinché abbia senso il radicale), ma anche f(x) risulterà positiva perché siamo sotto l’ipotesi in cui f(x) è maggiore della radice n-esima di g(x). Sotto queste ipotesi, è pertanto possibile elevare ancora una volta primo e secondo membro alla potenza n-esima e risolvere.
Per n pari si ha quindi la seguente soluzione
se n è pari
2° Caso – La disequazione irrazionale si trova nella forma
Se n è dispari basterà elevare, al solito, ambo i membri per la potenza n-esima così da potere risolvere la disequazione ottenuta, si avrà pertanto
| \[f(x)<\sqrt[n]{g(x)}\rightarrow\left[f(x)\right]^n<g(x)\] | se n dispari |
Se invece n risulta intero positivo pari osserviamo ancora una volta che dovrà risultare il radicando positivo, tuttavia la disequazione può essere stavolta verificata sia se f(x) è positiva, sia che f(x) risulti negativa.
Si ottengono così i seguenti sistemi risolventi:
Notiamo che nell’ultimo sistema (di destra) la seconda disequazione risulta implicitamente verificata dalla terza, infatti per n pari f(x) elevato ad un numero pari è certamente positivo e pertanto dovendo risultare g(x) maggiore della potenza n-esima di f(x) (che è positiva) sarà anche essa certamente positiva.
Tale ultimo sistema può quindi essere ridotto al seguente:
quando n è pari
Osservazioni
- Nel caso in cui f(x) è una costante a le disequazioni si riducono nella forma:
oppure
Nel caso di n dispari si procede alla risoluzione effettuando l’elevamento a potenza n-esima.
Nel caso di n pari bisogna ricordare che la radice n-esima di g(x) è, se esiste, positiva o nulla pertanto nelle ultime due equazioni è possibile elevare al quadrato soltanto se risulta a>0.
ESEMPI SVOLTI PASSO-PASSO: disequazioni irrazionali
ESEMPIO 1
Risolvere la seguente disequazione:
1) Dominio di definizione
La radice quadrata richiede che il radicando sia maggiore o uguale a zero e il denominatore diverso da zero:
Studiamo il segno della frazione:
- Il numeratore cambia segno in .
- Il denominatore cambia segno in .
Costruiamo una tabella di segno (solo logicamente, senza disegnare):
Per valori di :
- : numeratore
− , denominatore− ⇒ frazione positiva. - : numeratore
− , denominatore+ ⇒ frazione negativa. - : numeratore
+ , denominatore+ ⇒ frazione positiva.
Quindi la frazione è maggiore o uguale a zero per:
2) Effetto della radice quadrata
La radice quadrata è definita e reale solo quando il radicando è maggiore o uguale a zero, quindi il dominio effettivo della disequazione coincide con:
In tale dominio, la radice quadrata restituisce valori non negativi.
3) Analisi del segno
Poiché la radice quadrata di un numero non negativo è sempre maggiore o uguale a zero, la disequazione è sempre verificata nel dominio stesso.
4) Soluzione
Dunque la soluzione è:
ESEMPIO 2
Risolvere la seguente disequazione irrazionale:
1) Dominio di definizione
La radice quadrata è definita solo se il radicando è maggiore o uguale a zero:
Da cui si ricava:
2) Rimozione della radice
Poiché la funzione radice quadrata è crescente e restituisce solo valori non negativi, possiamo elevare al quadrato entrambi i membri senza cambiare il verso della disequazione (nel dominio definito):
3) Risoluzione della disequazione lineare
4) Intersezione con il dominio
Si devono soddisfare contemporaneamente:
Pertanto la soluzione è:
5) Verifica di coerenza
- Per x = 3/2: radicando = 0 ⇒ √0 = 0 < 7 ✅
- Per x = 26: radicando = 49 ⇒ √49 = 7 ❌ (non strettamente minore)
Conclusione: la disequazione è verificata per .
ESEMPIO 3
Risolvere la seguente disequazione:
1) Dominio di definizione
La radice cubica (indice dispari) è definita per tutti i numeri reali, dunque il dominio è .
2) Proprietà della funzione radice cubica
La funzione è monotona crescente su . Pertanto si può elevare al cubo ambo i membri senza cambiare il verso:
3) Semplificazione
Sviluppiamo il cubo a destra:
Sostituiamo nella disequazione:
4) Riduzione
Sottraiamo da entrambi i membri:
Moltiplichiamo per −1 (invertendo il verso):
ovvero:
Dividendo per 6:
5) Studio del segno
Fattorizziamo:
Il prodotto è negativo quando i due fattori hanno segno opposto, ossia per:
6) Soluzione
Gli estremi 0 e 2 non appartengono alla soluzione poiché la disuguaglianza è stretta.
ESEMPIO 4
Risolvere la seguente disequazione:
1) Dominio di definizione
Affinché entrambe le radici quadrate siano reali, i radicandi devono essere maggiori o uguali a zero:
e .
Il dominio comune è quindi:
2) Interpretazione della disequazione
All’interno del dominio, entrambi i termini e sono non negativi. La disequazione
è equivalente a , poiché si può sommare ad entrambi i membri.
3) Elevazione al quadrato
Poiché entrambe le radici sono non negative nel dominio, possiamo elevare al quadrato senza cambiare il verso:
Risolvendo:
4) Intersezione con il dominio
Intersecando la soluzione ottenuta con il dominio otteniamo:
Soluzione finale
Errori comuni da evitare
- Dimenticare il dominio.
Molti studenti risolvono la disequazione senza controllare il dominio e ottengono risultati errati. - Elevare al quadrato senza verificare i segni.
Ricorda: puoi elevare al quadrato una disuguaglianza solo se entrambi i membri sono non negativi. - Non controllare le soluzioni ottenute.
Dopo aver risolto, sostituisci i valori trovati nella disequazione iniziale per verificare che funzionino. - Semplificazioni scorrette con radici.
Evita di “togliere” la radice senza considerare la direzione della disequazione.
Come affrontare le disequazioni irrazionali nei test
Quando affronti un esercizio di questo tipo:
- Scrivi chiaramente il dominio.
- Isola la radice se necessario.
- Eleva al quadrato e semplifica con calma.
- Risolvi la disequazione risultante.
- Interseca la soluzione con il dominio iniziale.
- Controlla sempre le soluzioni trovate.
Riepilogo dei passaggi chiave
| Passaggio | Descrizione |
|---|---|
| 1. Dominio | Imporre che i radicandi siano ≥ 0 (solo per indice pari). |
| 2. Isolamento | Mettere una radice da una parte sola. |
| 3. Elevazione | Elevare al quadrato (o potenza pari). |
| 4. Risoluzione | Risolvere la disequazione risultante. |
| 5. Intersezione | Confrontare con il dominio iniziale. |
Esercizi riepilogativi
Prova a risolvere queste disequazioni irrazionali da solo
👉 Suggerimento: ricordati sempre il dominio prima di iniziare.
| Esercizio | Soluzione |
|---|---|
| x < 22 | |
| x ∈ [0.5, 3] | |
| x ∈ [2, 3.56] | |
| x ≥ 1 | |
| x < −2 oppure x > 3 |
Domande frequenti (FAQ)
Che cosa sono le disequazioni irrazionali?
Sono disequazioni in cui l’incognita compare sotto il segno di radice. Richiedono di considerare il dominio e di elevare al quadrato per eliminarla.
Posso sempre elevare al quadrato una disequazione irrazionale?
Solo se entrambe le parti sono non negative. Altrimenti il verso della disequazione può cambiare e si introducono soluzioni false.
Come si trova il dominio di una disequazione irrazionale?
Si impone che ogni radicando (cioè ciò che sta sotto la radice) sia maggiore o uguale a zero se la radice ha indice pari.
Quali sono le differenze tra equazioni e disequazioni irrazionali?
Le equazioni irrazionali cercano valori che rendono due espressioni uguali; le disequazioni stabiliscono invece un ordine (maggiore o minore) tra esse.
Conclusione
Le disequazioni irrazionali rappresentano un passo importante nell’algebra, perché uniscono la comprensione del dominio, le proprietà delle radici e la capacità di risolvere disequazioni di secondo grado.
Imparare a risolverle con metodo ti aiuta non solo negli esercizi di scuola, ma anche nella preparazione a test di ingresso universitari e concorsi.
Ricorda sempre:
- partire dal dominio,
- isolare la radice,
- elevare al quadrato con attenzione,
- intersecare le soluzioni con il dominio.
Con la pratica, questi passaggi diventeranno automatici.