Determinare l’equazione di una retta passante per due punti è uno dei problemi fondamentali della geometria analitica. Tale circostanza si verifica in moltissimi esercizi o problemi e costituisce la base per lo studio di parallelismo, perpendicolarità, fasci di rette, distanza di un punto da una retta, ma non solo.
In questo articolo vedremo in particolare due metodi generali per calcolare l’equazione della retta passante per due punti, con spiegazioni chiare, esempi svolti passo passo e i casi particolari da conoscere.
Il problema
Assegnati due punti distinti del piano cartesiano:
si vuole determinare l’equazione della retta che passa per entrambi i punti.
Per due punti distinti passa una e una sola retta.
Metodi per calcolare l’equazione della retta passante per due punti
Entrando nel dettaglio esporremo nel seguito due distinti metodi da poter utilizzare in maniera operativa per calcolare l’equazione di una retta passante per due punti.
In particolare tratteremo un primo metodo che consiste essenzialmente nel calcolo preliminare del coefficiente angolare della retta (noti che siano i punti A e B per cui la retta passa) oltre all’imposizione del passaggio per uno dei due punti (A o B). Successivamente andremo invece ad esporre un secondo metodo dove utilizzeremo un’equazione che consente direttamente il calcolo dell’equazione cartesiana a partire dalla conoscenza dei soli punti A e B.
Entrambi i metodi sono del tutto equivalenti e dovranno portare al medesimo risultato se applicati correttamente, come dimostreremo nel seguito. Vediamoli uno per uno!
Primo metodo: passaggio per un punto e coefficiente angolare noto
Richiamo teorico essenziale: il coefficiente angolare.
Il coefficiente angolare della retta che passa per i punti \(A(x_1,y_1)\) e \(B(x_2,y_2)\)
è dato da:
Esso rappresenta l’inclinazione della retta rispetto all’asse \(x\).
La formula per il calcolo di \(m\) è valida solo se \(x_1\) ed \(x_2\) sono diversi tra loro!
Il procedimento relativo al calcolo dell’equazione attraverso il passaggio per un punto e coefficiente angolare noto (primo metodo) si articola in tre passaggi che andiamo a descrivere nei punti a seguire:
1. Calcolo del coefficiente angolare
Si applica la formula:
che rappresenta il coefficiente angolare della retta passante per i punti \(A\) e \(B\).
2. Scelta della forma dell’equazione
Si utilizza l’equazione punto-pendenza nella forma:
Tale ultima equazione in sostanza può essere considerata come un caso particolare del fascio proprio di rette passanti per uno dei due punti A o B ma dove il coefficiente angolare m risulta noto.
3. Sostituzione dei valori numerici
Si sostituiscono le coordinate di uno dei due punti (indifferentemente A o B) ottenendo l’equazione cercata.
Dettaglio importante onde evitare equivoci:
se per esempio scegliamo di sostituire le coordinate del punto A avremo:
\(x_1=x_0\)
\(y_1=y_0\)
Se invece decidiamo, in alternativa, di sostituire le coordinate del punto B all’equazione punto-pendenza scriveremo:
\(x_2=x_0\)
\(y_2=y_0\)
Se si impone a questo punto il valore del coefficiente angolare è molto facile rendersi conto che quella ottenuta è proprio l’equazione ricercata.
⚠️ Attenzione: non è necessario imporre anche il passaggio per il secondo punto poiché se ne tiene già implicitamente conto attraverso il calcolo del coefficiente angolare \(m\).
Esempio svolto
Determinare l’equazione della retta passante per i punti:
Passo 1: calcolo del coefficiente angolare
Passo 2: forma punto–pendenza
Sostituendo all’equazione punto-pendenza il valore di \(m\) ed imponendo il passaggio per uno dei due punti, per esempio \(A\), si ottiene:
Passo 3: semplificazione
Infine si semplifica:
Equazione della retta:
Secondo metodo: equazione frazionaria della retta passante per due punti
Esiste un altro metodo, più diretto, per calcolare immediatamente l’equazione cartesiana della retta passante per due punti, in particolare è possibile fare uso della seguente formulazione chiamata forma simmetrica o frazionaria:
Se si prova ad applicare quest’ultima equazione all’esercizio svolto al paragrafo precedente, anche con questo altro metodo deve ottenersi la medesima equazione della retta come risultato finale.
Verifichiamo se ciò è vero.
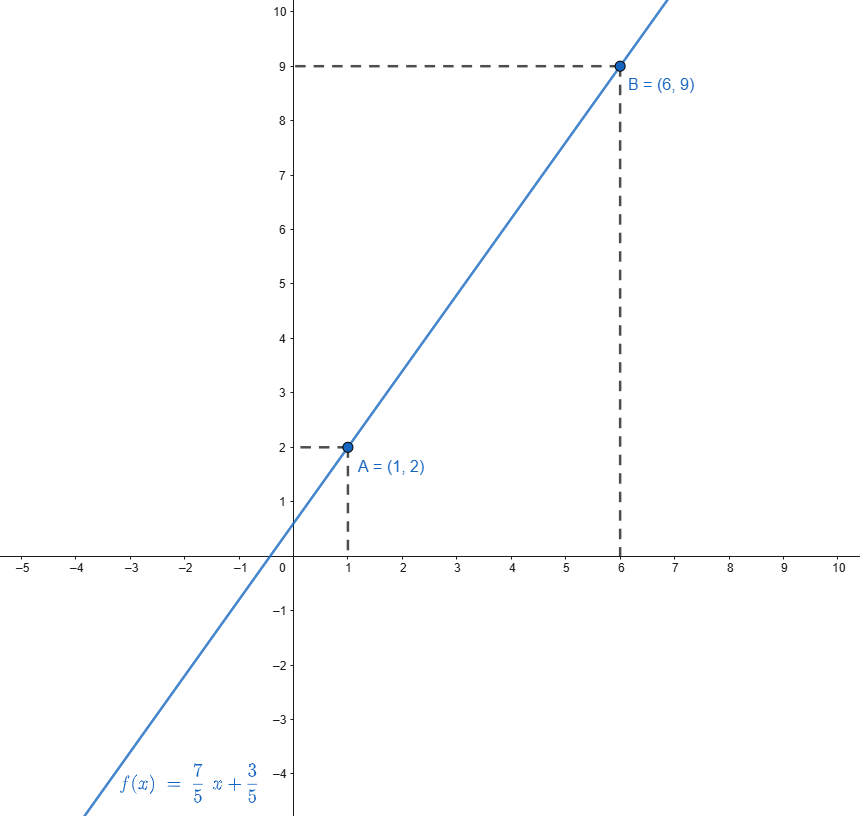
Punti: \(A(1,2)\) \(B(6,9)\)
Sostituiamo i valori numerici delle coordinate all’equazione in forma frazionaria ottenendo:
Semplificando si ottiene:
da cui
che è esattamente l’equazione ottenuta con il primo metodo (prima della semplificazione).
Adesso basterà semplificare (come nel Passo 3 del primo metodo) per ottenere esattamente il medesimo risultato finale:
Verifica del risultato
Sostituiamo le coordinate dei punti nell’equazione trovata:
- Per \(A(1,2)\): \(2 = 7/5 \cdot 1+3/5\) ✓
- Per \(B(6,9)\): \(9 = 7/5 \cdot 6+3/5\) ✓
La verifica è soddisfatta.
I procedimenti appena visti si basano sulle proprietà fondamentali della retta nel piano cartesiano, argomenti trattati in modo completo nell’articolo dedicato alla retta in geometria analitica.
Caso particolare: retta verticale
Se \(x_1 = x_2\), il coefficiente angolare non è definito.
In questo caso la retta è verticale e la sua equazione è:
Esempio
Se i punti sono:
l’equazione della retta passante per tali punti è:
Caso particolare: retta orizzontale
Se \(y_1 = y_2\), il coefficiente angolare è nullo:
In tal caso l’equazione della retta è:
Errori comuni da evitare
- Invertire le coordinate nella formula del coefficiente angolare
- Utilizzare formule inapplicabili quando \(x_1 = x_2\)
- Dimenticare di semplificare l’equazione finale
- Usare punti coincidenti
- Sbagliare i calcoli durante la semplificazione
Esercizi proposti con soluzione
- Determinare l’equazione della retta passante per i punti A(0,1) e B(2,5). [Soluzione: y=2x+1]
- Trovare l’equazione della retta passante per i punti A(-1,3) e B(2,3). [Soluzione: y=3]
- Determinare l’equazione della retta passante per i punti A(4,-2) e B(4,6). [Soluzione: x=4]
Conclusione
Saper determinare l’equazione di una retta passante per due punti è un passaggio essenziale nello studio della geometria analitica. I metodi sopra esposti vengono utilizzati in tantissimi contesti della matematica, fisica e della matematica applicata e costituiscono la base per la risoluzione di problemi geometrici ed analitici più complessi.