Il fascio proprio e improprio di rette è un argomento fondamentale della geometria analitica che permette di studiare insiemi di rette con una caratteristica comune: il passaggio per uno stesso punto oppure il parallelismo.
Comprendere la differenza tra queste due tipologie di fascio consente inoltre di risolvere con maggiore consapevolezza problemi su intersezioni, parallelismo, perpendicolarità e distanza tra punto e retta. In questa guida cercheremo di fornire definizioni chiare, formule generali ed esercizi svolti passo passo. In particolare vedremo:
- Cos’è un fascio di rette
- Differenza tra fascio proprio e fascio improprio
- Come scrivere l’equazione di ciascun tipo di fascio
- Esempi svolti passo passo
- Collegamenti con altri concetti della geometria analitica
Cos’è un fascio di rette
Un fascio di rette è un insieme di rette che condividono una caratteristica comune. Esistono due tipi principali di fascio:
- Fascio proprio – tutte le rette passano per uno stesso punto;
- Fascio improprio – tutte le rette sono parallele tra loro, quindi non si incontrano mai.
Fascio proprio di rette
Un fascio proprio è un insieme di rette che passano tutte per uno stesso punto \(P(x_0, y_0)\). Questo punto è chiamato centro del fascio.
Equazione generale
Consideriamo due rette distinte \(r_1\) ed \(r_2\) passanti per un punto \(P(x_0,y_0)\), comune ad entrambe.
Allora, qualsiasi retta del fascio si può scrivere come combinazione lineare delle due rette date \(r_1\) ed \(r_2\); in particolare, in forma implicita, si avrà:
Quest’ultima è la forma generale di un fascio proprio di rette.
In maniera del tutto equivalente, nella pratica risolutiva degli esercizi risulta spesso più agevole introdurre una forma più conveniente ed immediata rispetto alla (1), ricorrendo al concetto di coefficiente angolare \(m\):
Tale ultima equazione ci consente infatti di interpretare la retta appartenente al fascio proprio, come la generica retta \(r\) passante per il punto \(P(x_0,y_0)\), al variare del coefficiente angolare \(m\).
N.B. In generale, l’equazione di un fascio di rette può essere scritta in forma combinata, cioè come combinazione lineare di due rette assegnate (1). In questo modo, introducendo un parametro reale \(\lambda\), è possibile ottenere tutte le rette del fascio variando semplicemente il valore di tale parametro.
Esempio
Problema: Determinare l’equazione di tutte le rette passanti per \(P(2,3)\).
Soluzione:
Una retta generica passante per \(P\) ha equazione:
con \(m \in \mathbb{R}\).
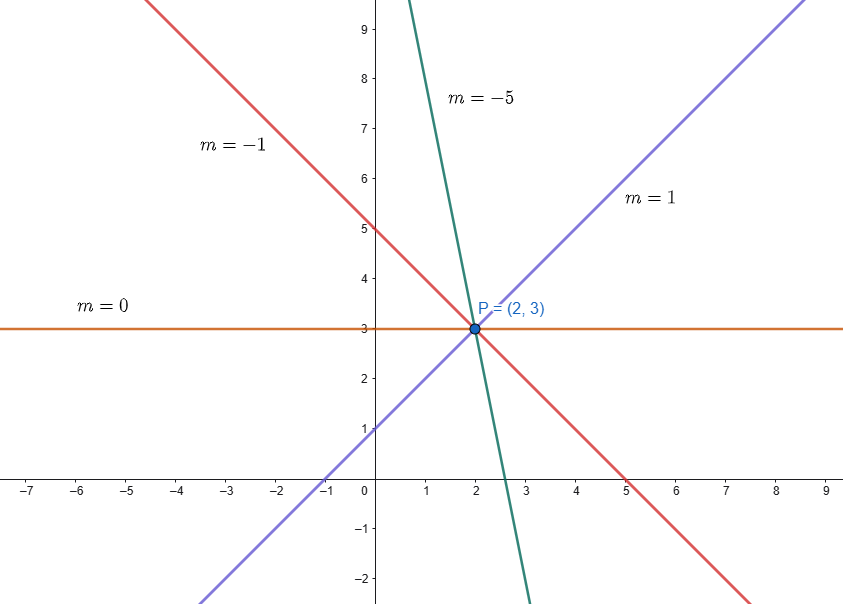
Tale equazione rappresenta l’equazione del fascio proprio di rette al variare di \(m\), come mostrato in Fig.1.
Analogamente, in forma implicita, possiamo scegliere due rette particolari:
ed ottenerne una rappresentazione attraverso una combinazione lineare.
Allora avremo che la forma combinata del fascio diventerà:
Interpretazione: Variando \(\lambda\), si ottengono tutte le rette che passano per \(P(2,3)\).
Fascio improprio di rette
Un fascio improprio di rette è un insieme di rette tutte parallele tra loro, quindi nessuna di esse si interseca. Se ne deduce pertanto immediatamente che tutte le rette del fascio improprio condividono lo stesso coefficiente angolare \(m\).
Equazione generale
Se si indica con \(m\) è il coefficiente angolare comune, la retta generica del fascio improprio può essere scritta in forma esplicita come:
oppure in forma implicita:
Esempio
Problema: Scrivere tutte le rette parallele a \(y=2x+1\).
Soluzione:
- Coefficiente angolare \(m\) = 2
- La retta generica del fascio può scriversi utilizzando la (3) come:
- Variando \(q\), otteniamo tutte le rette parallele a \(y = 2x + 1\) (Fig.2).
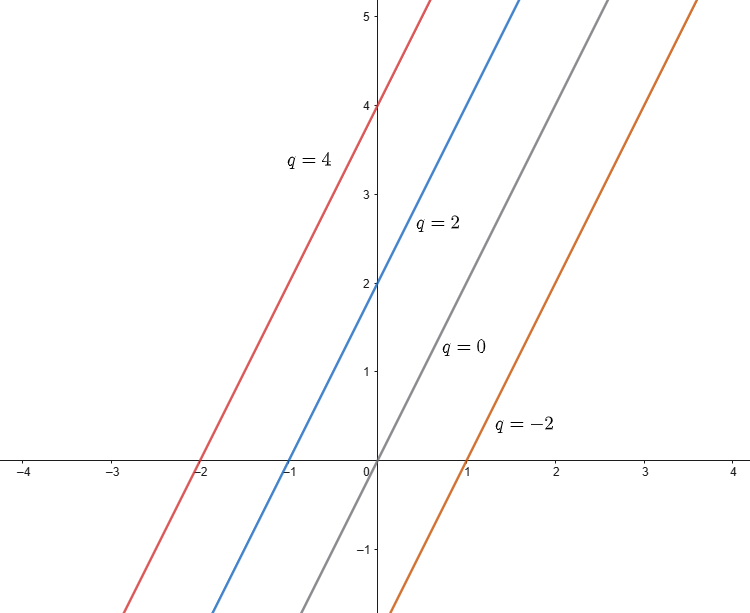
Interpretazione: Questo fascio non ha alcun punto in comune, infatti le rette non si incontrano mai.
Collegamenti con altri concetti della retta
Il concetto di fascio di rette si collega in modo naturale agli altri argomenti fondamentali della geometria analitica già trattati nel nostro percorso sulla retta ed in particolare con:
- Rette parallele e perpendicolari nel piano cartesiano → un fascio improprio è costituito da rette tutte parallele tra loro, mentre all’interno di un fascio proprio è sempre possibile individuare una retta perpendicolare a una retta assegnata.
- Coefficiente angolare della retta → ogni retta del fascio è caratterizzata da un proprio coefficiente angolare. Nel fascio improprio il coefficiente angolare è costante, mentre nel fascio proprio varia al variare del parametro \(m\) o \(\lambda\).
- Distanza di un punto da una retta → lo studio dei fasci di rette è utile per determinare quale retta del fascio realizza una distanza minima da un punto esterno.
- Equazione della retta passante per due punti → ogni retta di un fascio proprio può essere interpretata come la retta passante per il centro del fascio e un punto esterno qualsiasi del piano.
Se desideri una visione completa e organica sulla retta, ti consiglio di consultare la guida principale dedicata a La Retta in Geometria Analitica, dove troverai una trattazione sistematica dell’argomento, le proprietà ed alcune applicazioni.
Esercizi svolti passo passo
Esercizio 1: Fascio proprio
Problema: Determinare l’equazione del fascio proprio di rette passante per \(P(1,−2)\) e contenente la retta \(y=3x−5\).
Soluzione:
Utilizzando la (1) risulta immediato scrivere la combinazione lineare delle rette orizzontali e verticali passanti per \(P(1,-2)\).
La retta orizzontale per \(P\) risulta infatti l’equazione:
La retta verticale per \(P\) è rappresentata dall’equazione:
Ricorrendo alla (1) possiamo pertanto scrivere il fascio proprio di rette come:
Notiamo che è possibile pervenire ad analogo risultato anche utilizzando la forma (2), in tal caso si ottiene:
che rappresenta un analogo della combinazione lineare delle rette orizzontali e verticali passanti per \(P\) ove si è posto
Infine, per assicurarsi che la retta data sia contenuta nel fascio, basta osservare che per \(m=3\) l’equazione del fascio proprio fornisce la retta \(y=3x-5\).
Esercizio 2: Fascio improprio
Problema: Scrivere l’equazione del fascio di rette parallele a \(y = -\frac{1}{2}x + 1\) e passanti per un punto generico \(P(x_0, y_0)\).
Soluzione:
- Il coefficiente angolare della retta assegnata vale \(m = -\frac{1}{2}\)
- L’insieme delle rette parallele a quella data può ottenersi scrivendo l’equazione del fascio improprio come segue:
- Se vogliamo che passi per \(P(x_0, y_0)\), sostituendo le coordinate del punto \(P\) si ottiene:
- Sostituendo il valore di \(q\) all’equazione del fascio improprio, si ottiene l’equazione finale della retta passante per \(P\) e parallela alla retta data:
Consigli pratici
- Distinguere bene fascio proprio e improprio: spesso gli studenti confondono i due concetti; ricordarsi che il centro del fascio esiste solo nel proprio.
- Usare la forma combinata per fascio proprio, perché permette di generare tutte le rette al variare di un solo parametro \(\lambda\).
- Esercizi e grafici aiutano a visualizzare il fascio: il fascio proprio “converge” in un punto, quello improprio è “parallelo”.
Conclusione
I fasci di rette sono una naturale estensione dello studio della retta nel piano cartesiano costituendone un argomento centrale. Conoscere fascio proprio e improprio:
- permette di risolvere problemi avanzati di geometria analitica;
- consente di collegare algebra e geometria in maniera intuitiva;
- facilita la comprensione di intersezioni multiple e problemi di parallelismo/perpendicolarità.
Grazie agli esempi e agli esercizi svolti passo-passo, gli studenti dovrebbero poter visualizzare e comprendere immediatamente il comportamento delle rette in un fascio.