Il coefficiente angolare è uno dei concetti centrali della geometria analitica. Dal punto di vista geometrico, esso descrive l’inclinazione di una retta nel piano cartesiano; dal punto di vista analitico fornisce invece un’informazione fondamentale per lo studio dell’equazione della retta.
Comprenderne il significato e il procedimento di calcolo consente di interpretare correttamente l’equazione di una retta e di utilizzarla in modo appropriato e consapevole nello studio delle sue proprietà e nella risoluzione di problemi ed esercizi.
In questo articolo analizzeremo il coefficiente angolare in modo sistematico, dal significato geometrico al calcolo passo passo, accompagnando la trattazione con esempi svolti, grafici interattivi e l’analisi dei casi particolari. L’obiettivo è fornire una base solida e coerente per affrontare lo studio della retta con metodo e precisione.
Cos’è il coefficiente angolare di una retta
Il coefficiente angolare è una grandezza associata a una retta nel piano cartesiano che ne descrive l’inclinazione rispetto all’asse delle ascisse. Esso fornisce così un’informazione essenziale sul modo in cui una retta si dispone sul piano cartesiano e sul “comportamento” delle sue coordinate.
Dal punto di vista geometrico, il coefficiente angolare indica se la retta è crescente, decrescente o orizzontale e misura quanto rapidamente varia l’ordinata al variare dell’ascissa. Dal punto di vista analitico, rappresenta uno dei parametri fondamentali che caratterizza l’equazione della retta e che consente di collegare la sua rappresentazione grafica alla relativa espressione algebrica.
In questo senso, il coefficiente angolare costituisce un’informazione strutturale della retta, indispensabile per interpretarne l’equazione e per studiarne le proprietà.
Definizione di coefficiente angolare
Data una generica retta \(r\), si definisce coefficiente angolare di \(r\) il parametro costante \(m\) definito come il rapporto tra la variazione di ordinata, per unità di variazione di ascissa, in formule:
con
Alla luce di tale definizione è possibile effettuare immediatamente alcune considerazioni che andiamo ad esporre qui nel seguito:
- Se \(m>0\), la retta è crescente (all’aumentare di \(x\) aumentano anche i valori di \(y\))
- Se \(m<0\), la retta è decrescente (all’aumentare di \(x\) i valori di \(y\) diminuiscono)
- Se \(m=0\), la retta è orizzontale.
- Se la retta è verticale (parallela all’asse delle ordinate), il coefficiente angolare non è definito.
In altre parole, il coefficiente angolare ci indica quanto rapidamente la retta cresce o decresce in verticale al variare dell’ascissa.
Negli esempi a seguire cercheremo di capire meglio il concetto di retta crescente, decrescente, orizzontale e verticale ed il relativo legame con il coefficiente angolare.
Calcolo del coefficiente angolare
Se nel piano cartesiano si conoscono due punti distinti di coordinate \((x_1,y_1)\) e \((x_2, y_2)\) è possibile calcolare il coefficiente angolare come:
Esempio 1
Dati i punti di coordinate \(A(0,1)\) e \(B(3,7)\), determinare il coefficiente angolare della retta passante per tali punti. Si determini inoltre l’equazione della retta in forma esplicita.
SOLUZIONE
Per ottenere la soluzione basta applicare la (2), ottenendo:
Infine, per determinare l’equazione della retta nella forma esplicita (\(y=mx+q\)), basta osservare che il punto \(A\) giace sull’asse delle \(y\), pertanto l’ordinata di \(A\) coincide con \(q\); in formule risulta infatti che:
Sostituendo all’equazione della retta in forma esplicita si ottiene infine
Esempio 2
Dati i punti di coordinate \(C(-2,4)\) e \(D(1,-2)\) determinare il coefficiente angolare della retta passante per tali punti. Si determini inoltre l’equazione della retta in forma esplicita.
SOLUZIONE
Per ottenere la soluzione basta applicare nuovamente la (2), ottenendo questa volta:
Per determinare l’equazione della retta, procedendo come già visto nell’Esempio 1, si avrà:
L’equazione esplicitadella retta risulta pertanto pari a:
Significato geometrico del coefficiente angolare
Nel seguente paragrafo metteremo in evidenza la relazione tra il coefficiente angolare di una retta e la sua inclinazione (o pendenza). Le due grandezze sono infatti strettamente connesse.
RETTA CRESCENTE
Si considerino, a titolo di esempio, i punti A e B di coordinate note appartenenti alla retta di equazione \(y=x/2\) come in Fig.1.
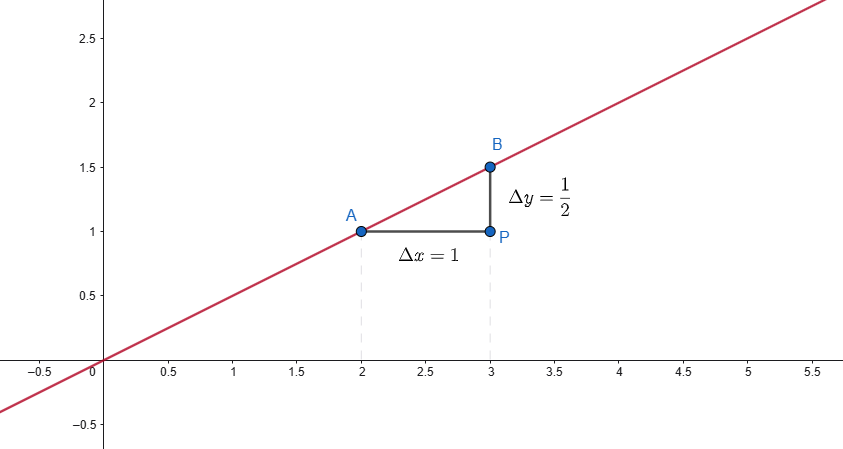
La retta è crescente.
In particolare, le coordinate dei punti risultano A(2,1) e B(3,3/2);
Calcolando gli incrementi risulta:
Applicando adesso la definizione (1) di coefficiente angolare si ha: \(\)
che è positivo.
Estendendo così il ragionamento al caso più generale possibile, si avrà che quando il coefficiente angolare \(m\) risulterà maggiore di zero, l’incremento di ordinate e l’incremento di ascisse saranno concordi, in formule:
Detto altrimenti:
il che significa che la retta è crescente (Fig.1).
⚠️ Il coefficiente angolare può essere pertanto interpretato come la variazione di ordinata quando la variazione di ascissa è unitaria, ma con una precisazione: a livello operativo (soprattutto nella risoluzione degli esercizi) non è necessario che la variazione di ascissa calcolata sia sempre unitaria, difatti, essendo il coefficiente angolare di una retta un parametro costante, questo può essere sempre calcolato come rapporto tra la variazione di ordinata e la variazione di ascissa (anche se la variazione di ascissa non è necessariamente unitaria!).
RETTA DECRESCENTE
Si considerino, a titolo di esempio, i punti e di coordinate note appartenenti alla retta di equazione \(y=-\frac{x}{3}\) come in Fig.2.
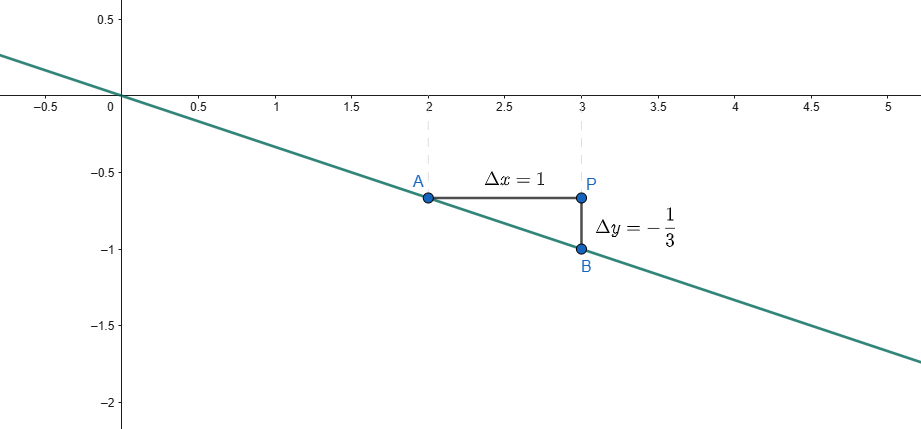
La retta è decrescente.
In particolare, le coordinate dei punti risultano:
\(A(2,-2/3)\)
\(B(3,-1)\)
Calcolando gli incrementi risulta che:
Applicando adesso la definizione (1) di coefficiente angolare si ottiene:
che risulta negativo.
Analogamente a quanto già visto in precedenza per la retta crescente ed estendendo al caso più generale anche quando il coefficiente angolare risulta negativo, si avrà che se il coefficiente angolare \(m\) è minore di zero, l’incremento di ordinate e l’incremento di ascisse saranno discordi tra loro, in formule:
Detto altrimenti:
il che significa che la retta è decrescente (Fig.2).
Casi particolari di coefficiente angolare: rette orizzontali e verticali
Le rette orizzontali (parallele all’asse \(x\)) e verticali (parallele all’asse \(y\)) costituiscono due casi particolari di calcolo del coefficiente angolare, in particolare dimostreremo che nel primo caso questo vale zero, mentre nel secondo caso il coefficiente angolare non risulta definito e pertanto non può essere calcolato.
Rette Orizzontali
In caso di retta orizzontale tutti i punti appartenenti alla retta hanno stessa ordinata; conseguentemente, a prescindere dalla variazione di ascissa \(x\), la variazione di ordinata è sempre nulla (\(\Delta y=0\)).
Ciò posto, applicando la definizione (1) e ponendo \(\Delta y=0\) si ottiene:
da cui consegue immediatamente che
Concludiamo che tutte le rette di equazione \(y=k\) (rette orizzontali) hanno coefficiente angolare nullo, in formule:
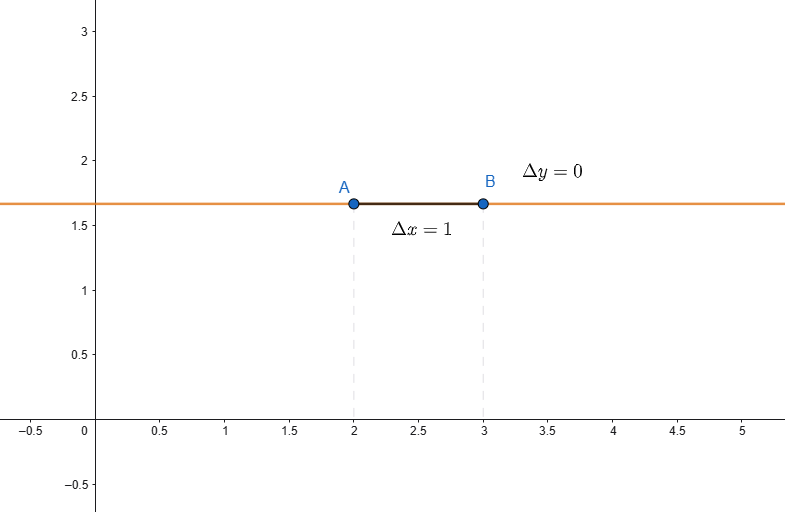
Si nota che la variazione di ordinata tra i punti A e B è uguale a zero, pertanto il coefficiente angolare risulta nullo.
Rette Verticali
In caso di retta verticale, tutti i punti appartenenti ad essa hanno la stessa ascissa, pertanto, indipendentemente dalla variazione di ordinata, la variazione di ascissa sarà sempre nulla.
Tuttavia, notiamo che in tale caso particolare si annullerebbe il denominatore della (1) facendola perdere di significato!
Concludiamo quindi che in caso di retta verticale (equazione generica \(x=h\)), il coefficiente angolare non risulta definito.
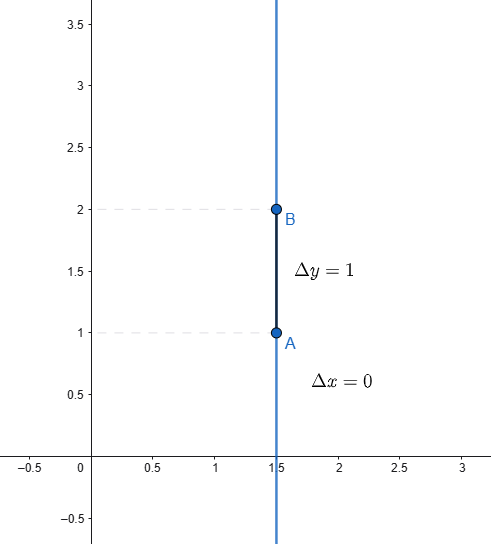
Si nota che la variazione di ascissa tra i punti A e B è uguale a zero, pertanto il coefficiente angolare non risulta definito.
Coefficiente angolare e forme dell’equazione della retta
Forma esplicita
Nella forma esplicita dell’equazione della retta il coefficiente angolare \(m\) figura all’interno dell’equazione:
- \(m\) = coefficiente angolare
- \(q\) = intercetta sull’asse y
Noto che sia quindi il valore di \(m\) e dell’ordinata dell’intercetta con l’asse delle ordinate \(q\), l’equazione della retta è immediatamente ricavabile.
Esempio: \(m=−1\), \(q=4\) → \(y=−x+4\)
Forma implicita
Nella forma implicita dell’equazione della retta, a differenza di quella esplicita, il coefficiente angolare non compare direttamente; dalla formulazione implicita risulta infatti che:
Tuttavia è possibile esplicitare tale equazione attraverso i seguenti passaggi:
- Passaggio alla forma esplicita: \(y=-\frac{A}{B}x – \frac{C}{B}\)
- Coefficiente angolare: \(−A/B\)
Esempio:
da cui
Forma parametrica
È noto che una retta può anche essere rappresentata nella generica forma parametrica, al variare del parametro reale \(t\) come segue:
In tal caso il coefficiente angolare è legato direttamente ai parametri direttivi e vale: \(m=b/a\) se \(a\neq 0\)
Esempio
Coefficiente angolare e rette parallele/perpendicolari
- Due rette parallele tra loro hanno lo stesso valore del coefficiente angolare \(m\)
- Due rette perpendicolari tra loro hanno coefficienti angolari l’uno l’opposto del reciproco dell’altro, in formule: \(m_1 \cdot m_2 = -1\)
Esempio numerico:
- Data la retta r: \(y=3x+2\) → \(m=3\)
- Esempio di una retta s parallela ad r: \(y=3x−1\)
- Esempio di una retta z perpendicolare ad r: \(y=-\frac{1}{3}x + 4\)
Grafico interattivo
Di seguito mostriamo il grafico interattivo di una generica retta di coefficiente angolare variabile e passante per il punto di coordinate (3,1).
Punto sulla retta:
x = 3, y = 1
Errori comuni
- Confondere \(Δy/Δx\) con \(Δx/Δy\)
- Applicare la formula per il calcolo di \(m\) anche ai casi di rette verticali
- Confondere coefficiente angolare con intercetta \(q\)
Applicazioni pratiche
Il concetto di coefficiente angolare trova applicazione in tantissimi ambiti come, a titolo di esempio:
- Modellazione lineare in fisica ed economia
- Analisi di pendenze (strade, rampe)
- Preparazione a problemi complessi di geometria
Collegamenti
Per una visione più completa della retta nel piano cartesiano, consigliamo di consultare il nostro articolo dedicato:
La Retta in Geometria Analitica: guida completa, equazioni e applicazioni
oppure puoi approfondire gli argomenti:
- Rette parallele e perpendicolari → per capire le inclinazioni e le relazioni di parallelismo ed ortogonalità tra rette;
- Equazione della retta passante per due punti → per calcolare direttamente l’equazione della retta (senza che sia necessario calcolare preliminarmente il coefficiente angolare).
Conclusione
Il coefficiente angolare non è semplicemente un numero: esso indica infatti la direzione della retta e mostra come algebra e geometria siano strettamente collegate tra loro. Comprenderne a fondo il significato consente di poter interpretare graficamente le rette, confrontarle e capirne le relazioni (come ad esempio parallelismo e perpendicolarità).
Questa conoscenza si intreccia naturalmente con altri argomenti matematici: ad esempio, permette di collegare le rette alle funzioni lineari, di analizzare variazioni e tassi di crescita e di comprendere concetti più avanzati come le pendenze in geometria analitica nello spazio o i problemi di massimo e minimo in analisi e molto altro.